Ovaj članak je o decimale. Ovdje ćemo razumjeti decimalni zapis razlomaka, uvesti pojam decimalnog razlomka i dati primjere decimalnih razlomaka. Zatim ćemo govoriti o znamenkama decimalnih razlomaka i dati nazive znamenki. Nakon ovoga, fokusirat ćemo se na beskonačne decimalne razlomke, razgovarajmo o periodičnim i neperiodskim razlomcima. U nastavku navodimo glavne radnje sa decimale. U zaključku, ustanovimo položaj decimalnih razlomaka na koordinatnoj gredi.
Navigacija po stranici.
Decimalni zapis razlomka broja
Čitanje decimala
Recimo nekoliko riječi o pravilima za čitanje decimalnih razlomaka.
Decimalni razlomci, koji odgovaraju pravim običnim razlomcima, čitaju se na isti način kao i ovi obični razlomci, samo se prvo dodaje "nula cijeli broj". Na primjer, decimalni razlomak 0,12 odgovara običnom razlomku 12/100 (čitaj „dvanaest stotinki“), stoga se 0,12 čita kao „nulta tačka dvanaest stotinki“.
Decimalni razlomci koji odgovaraju mješovitim brojevima čitaju se potpuno isto kao i ovi mješoviti brojevi. Na primjer, decimalni razlomak 56,002 odgovara mješovitom broju, tako da se decimalni razlomak 56,002 čita kao „pedeset šest zareza dvije hiljaditinke“.
Mjesta u decimalama
U pisanju decimalnih razlomaka, kao i u pisanju prirodni brojevi, značenje svake cifre zavisi od njenog položaja. Zaista, broj 3 u decimalnom razlomku 0,3 znači tri desetine, u decimalnom razlomku 0,0003 - tri desethiljaditinke, a u decimalnom razlomku 30.000,152 - tri desetine hiljada. Možemo razgovarati o tome decimalna mjesta, kao i o ciframa u prirodnim brojevima.
Nazivi cifara u decimalnom razlomku do decimalnog zareza potpuno se poklapaju sa nazivima cifara u prirodnim brojevima. A nazivi decimalnih mjesta iza decimalnog zareza mogu se vidjeti iz sljedeće tabele.

Na primjer, u decimalnom razlomku 37,051, cifra 3 je na mjestu desetica, 7 je na mjestu jedinica, 0 je na mjestu desetina, 5 je na mjestu stotinke, a 1 je na mjestu hiljaditih.
Mjesta u decimalnim razlomcima također se razlikuju po prioritetu. Ako se u pisanju decimalnog razlomka pomičemo s cifre na cifru s lijeva na desno, tada ćemo se kretati od seniori To junior ranks. Na primjer, mjesto stotine je starije od mjesta desetina, a mjesto miliona je niže od mjesta stotih. U datom konačnom decimalnom razlomku možemo govoriti o glavnim i sporednim ciframa. Na primjer, u decimalnom razlomku 604,9387 stariji (najviši) mjesto je mjesto stotine, i junior (najniži)- cifra desethiljaditih.
Za decimalne razlomke dolazi do proširenja u znamenke. Slično je proširenju u znamenke prirodnih brojeva. Na primjer, proširenje na decimalna mjesta od 45,6072 je kako slijedi: 45,6072=40+5+0,6+0,007+0,0002. A svojstva sabiranja iz dekompozicije decimalnog razlomka na znamenke omogućavaju vam da pređete na druge reprezentacije ovog decimalnog razlomka, na primjer, 45,6072=45+0,6072, ili 45,6072=40,6+5,007+0,0002, ili 45,6072= 72 0.6.
Završne decimale
Do sada smo govorili samo o decimalnim razlomcima u čijoj notaciji postoji konačan broj cifara iza decimalnog zareza. Takvi razlomci se nazivaju konačnim decimalima.
Definicija.
Završne decimale- To su decimalni razlomci, čiji zapisi sadrže konačan broj znakova (cifara).
Evo nekoliko primjera završnih decimalnih razlomaka: 0,317, 3,5, 51,1020304958, 230,032,45.
Međutim, ne može se svaki razlomak predstaviti kao konačna decimala. Na primjer, razlomak 5/13 ne može se zamijeniti jednakim razlomkom s jednim od nazivnika 10, 100, ..., stoga se ne može pretvoriti u konačni decimalni razlomak. O tome ćemo više govoriti u teorijskom dijelu, pretvarajući obične razlomke u decimale.
Beskonačne decimale: periodični razlomci i neperiodični razlomci
Pisanjem decimalnog razlomka nakon decimalnog zareza možete pretpostaviti mogućnost beskonačnog broja cifara. U ovom slučaju ćemo razmotriti takozvane beskonačne decimalne razlomke.
Definicija.
Beskonačne decimale- To su decimalni razlomci, koji sadrže beskonačan broj cifara.
Jasno je da beskonačne decimalne razlomke ne možemo zapisati u punom obliku, pa se u njihovom zapisivanju ograničavamo samo na određeni konačan broj cifara iza decimalnog zareza i stavljamo elipsu koja označava beskonačno kontinuirani niz cifara. Evo nekoliko primjera beskonačnih decimalnih razlomaka: 0,143940932…, 3,1415935432…, 153,02003004005…, 2,111111111…, 69,74152152152….
Ako pažljivo pogledate posljednja dva beskonačna decimalna razlomka, onda je u razlomku 2,111111111... jasno vidljiv broj 1 koji se beskrajno ponavlja, a u razlomku 69,74152152152..., počevši od treće decimale, grupa brojeva koja se ponavlja 1, 5 i 2 je jasno vidljiv. Takvi beskonačni decimalni razlomci nazivaju se periodični.
Definicija.
Periodične decimale(ili jednostavno periodične frakcije) su beskonačni decimalni razlomci kod kojih se, počevši od određenog decimalnog mjesta, beskonačno ponavlja neki broj ili grupa brojeva, što se naziva period razlomka.
Na primjer, period periodičnog razlomka 2,111111111... je cifra 1, a period razlomka 69,74152152152... je grupa cifara oblika 152.
Za beskonačne periodične decimalne razlomke je prihvaćeno poseban oblik evidencije. Radi kratkoće, dogovorili smo se da točku zapišemo jednom, stavljajući je u zagrade. Na primjer, periodični razlomak 2,111111111... je zapisan kao 2,(1) , a periodični razlomak 69,74152152152... je zapisan kao 69,74(152) .
Vrijedi napomenuti da za isti periodični decimalni razlomak možete odrediti različiti periodi. Na primjer, periodični decimalni razlomak 0,73333... može se smatrati razlomkom 0,7(3) sa periodom od 3, kao i razlomkom 0,7(33) sa periodom od 33, i tako dalje 0,7(333), 0,7 (3333), ... Periodični razlomak 0,73333 možete pogledati i ovako: 0,733(3), ili ovako 0,73(333), itd. Ovdje, da bismo izbjegli dvosmislenost i neslaganja, slažemo se da period decimalnog razlomka smatramo najkraćim od svih mogućih nizova cifara koje se ponavljaju, a počevši od najbliže pozicije decimalnoj zarezi. Odnosno, period decimalnog razlomka 0,73333... će se smatrati nizom od jedne cifre 3, a periodičnost počinje od druge pozicije nakon decimalnog zareza, odnosno 0,73333...=0,7(3). Drugi primjer: periodični razlomak 4,7412121212... ima period od 12, periodičnost počinje od treće cifre nakon decimalnog zareza, odnosno 4,7412121212...=4,74(12).
Beskonačni decimalni periodični razlomci se dobijaju kada se pretvore u decimalne razlomke obične frakcije, čiji imenioci sadrže proste faktore osim 2 i 5.
Ovdje je vrijedno spomenuti periodične razlomke sa periodom od 9. Navedimo primjere takvih razlomaka: 6.43(9) , 27, (9) . Ovi razlomci su još jedna oznaka za periodične razlomke s periodom 0 i obično se zamjenjuju periodičnim razlomcima s periodom 0. Da biste to učinili, period 9 se zamjenjuje periodom 0, a vrijednost sljedeće najviše cifre se povećava za jedan. Na primjer, razlomak s periodom 9 oblika 7.24(9) zamjenjuje se periodičnim razlomkom s periodom 0 oblika 7.25(0) ili jednakim konačnim decimalnim razlomkom 7.25. Drugi primjer: 4,(9)=5,(0)=5. Jednakost razlomka s periodom 9 i njegovog odgovarajućeg razlomka s periodom 0 lako se utvrđuje nakon zamjene ovih decimalnih razlomaka jednakim običnim razlomcima.
Na kraju, pogledajmo pobliže beskonačne decimalne razlomke, koji ne sadrže beskonačno ponavljajući niz cifara. Zovu se neperiodične.
Definicija.
Neponavljajuće decimale(ili jednostavno neperiodični razlomci) su beskonačni decimalni razlomci koji nemaju tačku.
Ponekad neperiodični razlomci imaju oblik sličan onom periodičnih razlomaka, na primjer, 8.02002000200002... je neperiodični razlomak. U tim slučajevima treba biti posebno oprezan da primijetite razliku.
Imajte na umu da se neperiodični razlomci ne pretvaraju u obične razlomke; beskonačni neperiodični decimalni razlomci predstavljaju iracionalne brojeve.
Operacije sa decimalama
Jedna od operacija s decimalnim razlomcima je poređenje, a definirane su i četiri osnovne aritmetičke funkcije operacije sa decimalama: sabiranje, oduzimanje, množenje i dijeljenje. Razmotrimo odvojeno svaku od radnji s decimalnim razlomcima.
Poređenje decimala u suštini zasnovan na poređenju običnih razlomaka koji odgovaraju decimalnim razlomcima koji se porede. Međutim, pretvaranje decimalnih razlomaka u obične razlomke je prilično naporan proces, a beskonačni neperiodični razlomci ne mogu se predstaviti kao obični razlomci, pa je zgodno koristiti poređenje decimalnih razlomaka po mjestu. Poređenje decimalnih razlomaka po mjestu slično je poređenju prirodnih brojeva. Za detaljnije informacije preporučujemo da proučite članak: poređenje decimalnih razlomaka, pravila, primjeri, rješenja.
Idemo dalje sledeća akcija - množenje decimala. Množenje konačnih decimalnih razlomaka vrši se slično oduzimanju decimalnih razlomaka, pravila, primjeri, rješenja množenja kolonom prirodnih brojeva. U slučaju periodičnih razlomaka, množenje se može svesti na množenje običnih razlomaka. Zauzvrat, množenje beskonačnih neperiodičnih decimalnih razlomaka nakon njihovog zaokruživanja svodi se na množenje konačnih decimalnih razlomaka. Preporučujemo za dalje proučavanje materijala u članku: množenje decimalnih razlomaka, pravila, primjeri, rješenja.
Decimale na koordinatnoj zraci
Postoji korespondencija jedan prema jedan između tačaka i decimala.
Hajde da shvatimo kako se konstruišu tačke na koordinatnoj zraci koje odgovaraju datom decimalnom razlomku.
Konačne decimalne razlomke i beskonačne periodične decimalne razlomke možemo zamijeniti jednakim običnim razlomcima, a zatim konstruirati odgovarajuće obične razlomke na koordinatnoj zraci. Na primjer, decimalni razlomak 1.4 odgovara običnom razlomku 14/10, tako da je tačka sa koordinatom 1.4 uklonjena iz ishodišta u pozitivnom smjeru za 14 segmenata jednakih desetini jediničnog segmenta.

Decimalni razlomci se mogu označiti na koordinatnoj zraci, počevši od dekompozicije datog decimalnog razlomka na znamenke. Na primjer, trebamo izgraditi tačku sa koordinatom 16.3007, pošto je 16.3007=16+0.3+0.0007, onda možemo doći do ove tačke uzastopnim polaganjem 16 jediničnih segmenata od početka koordinata, 3 segmenta čija je dužina jednaka desetoj jedinice i 7 segmenata čija je dužina jednaka desetohiljaditom dijelu jediničnog segmenta.
Ovakav način gradnje decimalni brojevi na koordinatnoj zraci omogućava vam da se približite koliko god želite tački koja odgovara beskonačnom decimalnom razlomku.
Ponekad je moguće precizno iscrtati tačku koja odgovara beskonačnom decimalnom razlomku. Na primjer, ![]() , tada ovaj beskonačni decimalni razlomak 1,41421... odgovara tački na koordinatnoj zraci, udaljenoj od početka koordinata dužinom dijagonale kvadrata sa stranicom od 1 jediničnog segmenta.
, tada ovaj beskonačni decimalni razlomak 1,41421... odgovara tački na koordinatnoj zraci, udaljenoj od početka koordinata dužinom dijagonale kvadrata sa stranicom od 1 jediničnog segmenta.
Obrnuti proces dobijanja decimalnog razlomka koji odgovara datoj tački na koordinatnoj zraci je tzv. decimalno mjerenje segmenta. Hajde da shvatimo kako se to radi.
Neka naš zadatak bude da dođemo od početka do date tačke na koordinatnoj liniji (ili da joj se beskonačno približimo ako ne možemo do nje). Kod decimalnog mjerenja segmenta, možemo sekvencijalno od početka odbaciti bilo koji broj jediničnih segmenata, zatim segmenata čija je dužina jednaka desetinki jedinice, zatim segmenata čija je dužina jednaka stotom dijelu jedinice, itd. Zapisivanjem broja segmenata svake dužine položenih, dobijamo decimalni razlomak koji odgovara datoj tački na koordinatnoj zraci.
Na primjer, da biste došli do tačke M na gornjoj slici, morate izdvojiti 1 jedinični segment i 4 segmenta, čija je dužina jednaka desetini jedinice. Dakle, tačka M odgovara decimalnom razlomku 1.4.
Jasno je da tačke koordinatnog zraka, koje se ne mogu dostići u procesu decimalnog mjerenja, odgovaraju beskonačnim decimalnim razlomcima.
Bibliografija.
- Matematika: udžbenik za 5. razred. opšte obrazovanje institucije / N. Ya. Vilenkin, V. I. Zhokhov, A. S. Chesnokov, S. I. Shvartsburd. - 21. izdanje, izbrisano. - M.: Mnemosyne, 2007. - 280 str.: ilustr. ISBN 5-346-00699-0.
- Matematika. 6. razred: vaspitni. za opšte obrazovanje institucije / [N. Ya. Vilenkin i drugi]. - 22. izdanje, rev. - M.: Mnemosyne, 2008. - 288 str.: ilustr. ISBN 978-5-346-00897-2.
- algebra: udžbenik za 8. razred. opšte obrazovanje institucije / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; uređeno od S. A. Telyakovsky. - 16. ed. - M.: Obrazovanje, 2008. - 271 str. : ill. - ISBN 978-5-09-019243-9.
- Gusev V. A., Mordkovich A. G. Matematika (priručnik za polaznike tehničkih škola): Proc. dodatak.- M.; Više škola, 1984.-351 str., ilustr.
Kao što je poznato, skup racionalnih brojeva (Q) uključuje skup cijelih brojeva (Z), koji zauzvrat uključuje skup prirodnih brojeva (N). Osim cijelih brojeva, racionalni brojevi uključuju razlomke.
Zašto se onda čitav skup racionalnih brojeva ponekad smatra beskonačnim periodičnim decimalnim razlomcima? Zaista, osim razlomaka, oni uključuju i cijele brojeve, kao i neperiodične razlomke.
Činjenica je da se svi cijeli brojevi, kao i bilo koji razlomak, mogu predstaviti kao beskonačan periodični decimalni razlomak. To jest, za sve racionalne brojeve možete koristiti isti metod snimanja.
Kako je predstavljena beskonačna periodična decimala? U njemu se ponavljajuća grupa brojeva iza decimalnog zareza stavlja u zagrade. Na primjer, 1,56(12) je razlomak u kojem se ponavlja grupa cifara 12, tj. razlomak ima vrijednost 1,561212121212... i tako u nedogled. Grupa brojeva koja se ponavlja naziva se tačka.
Međutim, u ovom obliku možemo predstaviti bilo koji broj ako smatramo da je njegov period broj 0, koji se takođe beskrajno ponavlja. Na primjer, broj 2 je isti kao 2,00000.... Dakle, može se napisati kao beskonačan periodični razlomak, tj. 2,(0).
Isto se može učiniti sa bilo kojim konačnim razlomkom. Na primjer:
0,125 = 0,1250000... = 0,125(0)
Međutim, u praksi ne koriste transformaciju konačnog razlomka u beskonačan periodični. Stoga odvajaju konačne razlomke i beskonačne periodične. Stoga je ispravnije reći da racionalni brojevi uključuju
- svi cijeli brojevi
- završni razlomci,
- beskonačni periodični razlomci.
U isto vrijeme, jednostavno zapamtite da su cijeli brojevi i konačni razlomci u teoriji predstavljeni u obliku beskonačnih periodičnih razlomaka.
S druge strane, koncepti konačnih i beskonačni razlomak primjenjivo na decimalne razlomke. Kada su u pitanju razlomci, i konačne i beskonačne decimale mogu se jedinstveno predstaviti kao razlomak. To znači da su sa stanovišta običnih razlomaka, periodični i konačni razlomci ista stvar. Osim toga, cijeli brojevi se također mogu predstaviti kao razlomak tako što ćemo zamisliti da broj dijelimo sa 1.
Kako predstaviti decimalni beskonačni periodični razlomak kao običan razlomak? Algoritam koji se najčešće koristi je otprilike ovaj:
- Smanjite razlomak tako da iza decimalnog zareza bude samo tačka.
- Pomnožite beskonačan periodični razlomak sa 10 ili 100 ili ... tako da se decimalni zarez pomjeri udesno za jednu tačku (tj. jedna tačka završi u cijelom dijelu).
- Izjednačite originalni razlomak (a) sa promjenljivom x, a razlomak (b) dobiven množenjem sa brojem N do Nx.
- Oduzmi x od Nx. Od b oduzimam a. To jest, oni čine jednačinu Nx – x = b – a.
- Prilikom rješavanja jednadžbe rezultat je običan razlomak.
Primjer pretvaranja beskonačnog periodičnog decimalnog razlomka u običan razlomak:
x = 1,13333...
10x = 11,3333...
10x * 10 = 11,33333... * 10
100x = 113,3333...
100x – 10x = 113,3333... – 11,3333...
90x = 102
x =
Da biste racionalni broj m/n zapisali kao decimalni razlomak, trebate podijeliti brojilac sa nazivnikom. U ovom slučaju, količnik se zapisuje kao konačan ili beskonačan decimalni razlomak.
Zapiši dati broj kao decimalni razlomak.
Rješenje. Podijelite brojilac svakog razlomka u kolonu po nazivniku: A) podijeliti 6 sa 25; b) podijeliti 2 sa 3; V) podijelite 1 sa 2, a zatim dodajte dobijeni razlomak na jedan - cijeli broj ovog mješovitog broja.

Nesvodljivi obični razlomci čiji imenioci ne sadrže proste faktore osim 2 I 5 , zapisuju se kao konačni decimalni razlomak.
IN primjer 1 kada A) imenilac 25=5·5; kada V) imenilac je 2, pa dobijamo konačne decimale 0,24 i 1,5. Kada b) imenilac je 3, tako da se rezultat ne može zapisati kao konačna decimala.
Da li je moguće, bez dugog dijeljenja, pretvoriti u decimalni razlomak takav običan razlomak, čiji nazivnik ne sadrži druge djelitelje osim 2 i 5? Hajde da to shvatimo! Koji se razlomak naziva decimalom i piše se bez razlomka? Odgovor: razlomak sa nazivnikom 10; 100; 1000 itd. I svaki od ovih brojeva je proizvod jednaka broj dvojki i petica. U stvari: 10=2 ·5 ; 100=2 ·5 ·2 ·5 ; 1000=2 ·5 ·2 ·5 ·2 ·5 itd.
Posljedično, nazivnik nesmanjivog običnog razlomka morat će se predstaviti kao proizvod "dvojke" i "petice", a zatim pomnožiti sa 2 i (ili) 5 tako da "dvojke" i "petice" postanu jednake. Tada će imenilac razlomka biti jednak 10 ili 100 ili 1000, itd. Da bismo osigurali da se vrijednost razlomka ne promijeni, pomnožimo brojilac razlomka istim brojem kojim smo pomnožili imenilac.
Izrazite sljedeće obične razlomke kao decimale:
![]()
Rješenje. Svaki od ovih razlomaka je nesvodljiv. Razložimo imenilac svakog razlomka u proste faktore.
20=2·2·5. Zaključak: nedostaje jedno "A".
8=2·2·2. Zaključak: nedostaju tri "A".
25=5·5. Zaključak: nedostaju dvije “dvojke”.

Komentar. U praksi često ne koriste faktorizaciju nazivnika, već jednostavno postavljaju pitanje: sa koliko treba pomnožiti imenilac da bi rezultat bio jedan sa nulama (10 ili 100 ili 1000 itd.). I tada se brojilac množi sa istim brojem.
Dakle, u slučaju A)(primjer 2) od broja 20 možete dobiti 100 množenjem sa 5, dakle, trebate pomnožiti brojilac i imenilac sa 5.
Kada b)(primjer 2) iz broja 8 neće se dobiti broj 100, ali će se broj 1000 dobiti množenjem sa 125. I brojnik (3) i imenilac (8) razlomka se množe sa 125.
Kada V)(primjer 2) od 25 dobijete 100 ako pomnožite sa 4. To znači da se brojilac 8 mora pomnožiti sa 4.
Poziva se beskonačni decimalni razlomak u kojem se jedna ili više cifara uvijek ponavlja u istom nizu periodično kao decimalni. Skup cifara koje se ponavljaju naziva se period ovog razlomka. Radi kratkoće, period razlomka se piše jednom, u zagradama.
Kada b)(primjer 1) postoji samo jedna cifra koja se ponavlja i jednaka je 6. Dakle, naš rezultat 0,66... biće napisan ovako: 0,(6) . Čitaju: nula poena, šest u tački.
Ako postoji jedna ili više cifara koje se ne ponavljaju između decimalnog zareza i prve tačke, onda se takav periodični razlomak naziva mješoviti periodični razlomak.
Nesvodljivi obični razlomak čiji je imenilac zajedno sa drugima množitelj sadrži množitelj 2 ili 5 , postaje mješovito periodični razlomak.
Zapišite brojeve kao decimalni razlomak:
![]()
Svaki racionalni broj može se napisati kao beskonačan periodični decimalni razlomak.
Zapišite brojeve kao beskonačan periodični razlomak.
Sjećate se kako sam u prvoj lekciji o decimalima rekao da postoje brojčani razlomci koji se ne mogu predstaviti kao decimale (pogledajte lekciju “Decimale”)? Takođe smo naučili kako da rastavljamo nazivnike razlomaka da vidimo da li postoje drugi brojevi osim 2 i 5.
Dakle: lagao sam. A danas ćemo naučiti kako pretvoriti apsolutno bilo koji brojčani razlomak u decimalni. Istovremeno ćemo se upoznati s cijelom klasom razlomaka sa beskonačnim značajnim dijelom.
Periodična decimala je svaka decimala koja:
- Značajni dio se sastoji od beskonačnog broja cifara;
- U određenim intervalima ponavljaju se brojevi u značajnom dijelu.
Skup cifara koji se ponavljaju koji čine značajan dio naziva se periodični dio razlomka, a broj cifara u ovom skupu se naziva periodom razlomka. Preostali segment značajnog dijela, koji se ne ponavlja, naziva se neperiodični dio.
Budući da postoji mnogo definicija, vrijedno je razmotriti nekoliko od ovih razlomaka detaljno:
Ovaj razlomak se najčešće pojavljuje u problemima. Neperiodični dio: 0; periodični dio: 3; dužina perioda: 1.
Neperiodični dio: 0,58; periodični dio: 3; dužina perioda: ponovo 1.
Neperiodični dio: 1; periodični dio: 54; dužina perioda: 2.
Neperiodični dio: 0; periodični dio: 641025; dužina perioda: 6. Radi praktičnosti, dijelovi koji se ponavljaju odvojeni su jedan od drugog razmakom - to nije potrebno u ovom rješenju.
Neperiodični dio: 3066; periodični dio: 6; dužina perioda: 1.
Kao što vidite, definicija periodičnog razlomka zasniva se na konceptu značajan dio broja. Stoga, ako ste zaboravili šta je to, preporučujem da to ponovite - pogledajte lekciju “”.
Prijelaz na periodični decimalni razlomak
Razmotrimo običan razlomak oblika a /b. Razložimo njegov imenilac u proste faktore. Postoje dvije opcije:
- Proširivanje sadrži samo faktore 2 i 5. Ovi razlomci se lako pretvaraju u decimale - pogledajte lekciju “Decimale”. Takvi ljudi nas ne zanimaju;
- Postoji još nešto u proširenju osim 2 i 5. U ovom slučaju, razlomak se ne može predstaviti kao decimalni, ali se može pretvoriti u periodičnu decimalu.
Da biste definirali periodični decimalni razlomak, morate pronaći njegove periodične i neperiodične dijelove. Kako? Pretvorite razlomak u nepravilan razlomak, a zatim podijelite brojilac sa nazivnikom koristeći ugao.
dogodit će se sljedeće:
- Prvo će se razdvojiti cijeli dio , ako postoji;
- Može biti nekoliko brojeva iza decimalnog zareza;
- Nakon nekog vremena brojevi će početi ponovi.
To je sve! Brojevi koji se ponavljaju iza decimalnog zareza označavaju se periodičnim dijelom, a oni ispred neperiodičnih.
Zadatak. Pretvorite obične razlomke u periodične decimale:
Svi razlomci bez celobrojnog dela, tako da jednostavno podelimo brojilac sa nazivnikom sa "uglom":

Kao što vidite, ostaci se ponavljaju. Zapišimo razlomak u “tačnom” obliku: 1,733 ... = 1,7(3).

Rezultat je razlomak: 0,5833 ... = 0,58(3).

Pišite na normalna forma: 4,0909 ... = 4,(09).

Dobijamo razlomak: 0,4141 ... = 0.(41).
Prijelaz s periodičnog decimalnog razlomka na obični razlomak
Razmotrimo periodični decimalni razlomak X = abc (a 1 b 1 c 1). Potrebno ga je pretvoriti u klasičnu "dvokatnicu". Da biste to učinili, slijedite četiri jednostavna koraka:
- Pronađite period razlomka, tj. izbroji koliko je cifara u periodičnom dijelu. Neka je ovo broj k;
- Odrediti vrijednost izraza X · 10 k. Ovo je ekvivalentno pomicanju decimalne točke za puni period desno - pogledajte lekciju “Množenje i dijeljenje decimala”;
- Originalni izraz mora se oduzeti od rezultirajućeg broja. U ovom slučaju, periodični dio je "spaljen" i ostaje običan razlomak;
- Pronađite X u rezultirajućoj jednadžbi. Sve decimalne razlomke pretvaramo u obične razlomke.
Zadatak. Smanjite na obično nepravilan razlomak brojevi:
- 9,(6);
- 32,(39);
- 0,30(5);
- 0,(2475).
Radimo s prvim razlomkom: X = 9, (6) = 9,666 ...
Zagrade sadrže samo jednu cifru, tako da je period k = 1. Zatim ovaj razlomak pomnožimo sa 10 k = 10 1 = 10. Imamo:
10X = 10 9,6666... = 96,666...
Oduzmite originalni razlomak i riješite jednačinu:
10X − X = 96,666 ... − 9,666 ... = 96 − 9 = 87;
9X = 87;
X = 87/9 = 29/3.
Pogledajmo sada drugi razlomak. Dakle, X = 32, (39) = 32,393939...
Period k = 2, pa pomnožite sve sa 10 k = 10 2 = 100:
100X = 100 · 32,393939 ... = 3239,3939 ...
Ponovo oduzmite prvobitni razlomak i riješite jednačinu:
100X − X = 3239,3939 ... − 32,3939 ... = 3239 − 32 = 3207;
99X = 3207;
X = 3207/99 = 1069/33.
Pređimo na treći razlomak: X = 0,30(5) = 0,30555... Dijagram je isti, pa ću samo dati proračune:
Period k = 1 ⇒ pomnožiti sve sa 10 k = 10 1 = 10;
10X = 10 0,30555... = 3,05555...
10X − X = 3,0555 ... − 0,305555 ... = 2,75 = 11/4;
9X = 11/4;
X = (11/4) : 9 = 11/36.
Konačno, posljednji razlomak: X = 0, (2475) = 0,2475 2475... Opet, radi pogodnosti, periodični dijelovi su odvojeni jedan od drugog razmacima. Imamo:
k = 4 ⇒ 10 k = 10 4 = 10.000;
10,000X = 10,000 0,2475 2475 = 2475,2475 ...
10,000X − X = 2475,2475 ... − 0,2475 2475 ... = 2475;
9999X = 2475;
X = 2475: 9999 = 25/101.
Beskonačne decimale
Decimale iza decimalnog zareza mogu sadržavati beskonačan broj cifara.
Beskonačne decimale- to su decimalni razlomci, koji sadrže beskonačan broj cifara.
Beskonačan decimalni razlomak je gotovo nemoguće u potpunosti zapisati, pa se pri njihovom pisanju ograničavaju na samo određeni konačan broj cifara iza decimalnog zareza, nakon čega se stavlja elipsa, što označava beskonačno kontinuirani niz cifara.
Primjer 1
Na primjer, $0.443340831\dots ; 3.1415935432\dots ; 135.126730405\dots ; 4.33333333333\dots ; 676.68349349\dots$.
Pogledajmo posljednje dvije beskonačne decimale. U razlomku $4.33333333333\dots$ cifra $3$ se ponavlja beskonačno, a u razlomku $676.68349349\dots$ grupa cifara $3$, $4$ i $9$ se ponavlja od treće decimale. Takvi beskonačni decimalni razlomci nazivaju se periodični.
Periodične decimale
Periodične decimale(ili periodične frakcije) su beskonačni decimalni razlomci, u čijem se zapisu neki broj ili grupa brojeva, nazvana periodom razlomka, beskonačno ponavlja sa određenog decimalnog mjesta).
Primjer 2
Na primjer, period periodičnog razlomka $4,33333333333\dots$ je znamenka $3$, a period razlomka $676,68349349\dots$ je grupa cifara $349$.
Radi kratkoće pisanja beskonačnih periodičnih decimalnih razlomaka, uobičajeno je da se tačka napiše jednom, stavljajući je u zagrade. Na primjer, periodični razlomak $4.33333333333\dots$ je napisan $4,(3)$, a periodični razlomak $676.68349349\dots$ je napisan $676.68(349)$.
Beskonačni periodični decimalni razlomci se dobijaju pretvaranjem običnih razlomaka čiji imenioci sadrže proste faktore osim $2$ i $5$ u decimalne razlomke.
Bilo koji konačni decimalni razlomak (i cijeli broj) može se napisati kao periodični razlomak dodavanjem beskonačnog broja cifara $0$ desno.
Primjer 3
Na primjer, konačna decimalna jedinica $45,12$ mogla bi se napisati kao periodični razlomak kao $45,12(0)$, a cijeli broj $(74)$ kao beskonačna periodična decimala bi bila $74(0)$.
U slučaju periodičnih razlomaka koji imaju period od 9, koristite prijelaz na drugu notaciju periodičnog razlomka s periodom od $0$. Samo u tu svrhu, period 9 se zamjenjuje točkom $0$, a vrijednost sljedeće najviše cifre se povećava za $1$.
Primjer 4
Na primjer, periodični razlomak $7,45(9)$ može se zamijeniti periodičnim razlomkom $7,46(0)$ ili ekvivalentnim decimalnim razlomkom $7,46$.
Beskonačni decimalni periodični razlomci su predstavljeni racionalnim brojevima. Drugim riječima, bilo koji periodični razlomak se može pretvoriti u običan razlomak, a svaki obični razlomak se može predstaviti kao periodični razlomak.
Pretvaranje razlomaka u konačne i beskonačne periodične decimale
Ne samo da se obični razlomci sa nazivnicima $10, 100, \dots$ mogu pretvoriti u decimalni razlomak.
U nekim slučajevima, originalni obični razlomak se lako može svesti na nazivnik od $10$, $100$ ili $1\000$, nakon čega se rezultujući razlomak može predstaviti kao decimalni razlomak.
Primjer 5
Da biste pretvorili razlomak $\frac(3)(5)$ u razlomak sa nazivnikom $10$, potrebno je pomnožiti brojilac i imenilac razlomka sa $2$, nakon čega dobijamo $\frac(6)( 10)$, što nije teško prevesti u decimalni razlomak $0,6$.
Za druge slučajeve koristi se druga metoda pretvaranja običnog razlomka u decimalu):
brojilac mora biti zamijenjen decimalnim razlomkom sa bilo kojim brojem nula iza decimalne točke;
podijeliti brojilac razlomka sa nazivnikom (podjela se vrši kao dijeljenje prirodnih brojeva u kolonu, a u količniku se nakon završetka dijeljenja cijelog dijela dividende stavlja decimalna točka).
Primjer 6
Pretvorite razlomak $\frac(621)(4)$ u decimalu.
Rješenje.
Predstavimo broj $621$ u brojiocu kao decimalni razlomak. Da biste to učinili, dodajte decimalni zarez i, za početak, dvije nule iza nje. Zatim, ako je potrebno, možete dodati još nula. Dakle, dobili smo 621,00$.
Podijelimo broj $621.00$ sa $4$ u kolonu:
Slika 1.
Podjela je dostigla decimalni zarez u dividendi, a ostatak nije bio nula. U ovom slučaju, decimalni zarez se stavlja u količnik i dijeljenje se nastavlja u koloni, bez obzira na zareze:
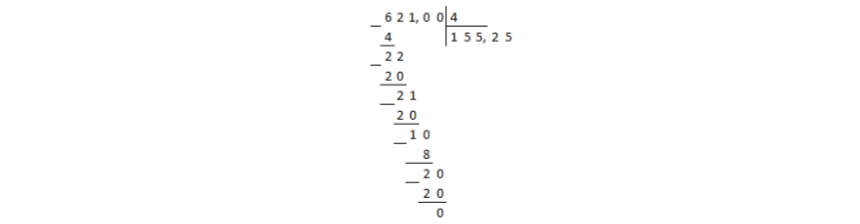
Slika 2.
Ostatak je nula, što znači da je podjela završena.
Odgovori: $155,25$.
Moguće je da prilikom dijeljenja brojnika i nazivnika običnog razlomka, ostatak ne rezultira u $0$. U ovom slučaju, podjela se može nastaviti na neodređeno vrijeme. Počevši od određenog trenutka, ostaci od dijeljenja se periodično ponavljaju, što znači da se ponavljaju i brojevi u količniku. Iz ovoga možemo zaključiti da će se ovaj obični razlomak pretvoriti u beskonačan periodični decimalni razlomak.
Primjer 7
Pretvorite razlomak $\frac(19)(44)$ u decimalu.
Rješenje.)
Da konvertujete obični razlomak u decimalu, izvršite dugo dijeljenje:

Slika 3.
Kod dijeljenja se ponavljaju ostaci $8$ i $36$, au količniku se također ponavljaju brojevi $1$ i $8$. Dakle, originalni obični razlomak $\frac(19)(44)$ je pretvoren u periodični razlomak $\frac(19)(44)=0.43181818\dots =0.43(18)$.
odgovor: $0,43(18)$.
Opšti zaključak o pretvaranju običnih razlomaka u decimale:
ako se imenilac može razložiti na proste faktore, među kojima će biti prisutni samo brojevi $2$ i $5$, onda se takav razlomak može pretvoriti u konačni decimalni razlomak;
ako, pored brojeva $2$ i $5$, proširenje nazivnika sadrži i druge proste brojeve, tada se takav razlomak pretvara u beskonačan decimalni periodični razlomak.

