Instructions
We determine the angular coefficient of the tangent to the curve at point M.
The curve representing the graph of the function y = f(x) is continuous in a certain neighborhood of the point M (including the point M itself).
If the value f‘(x0) does not exist, then either there is no tangent, or it runs vertically. In view of this, the presence of a derivative of the function at the point x0 is due to the existence of a non-vertical tangent tangent to the graph of the function at the point (x0, f(x0)). In this case, the angular coefficient of the tangent will be equal to f "(x0). Thus, the geometric meaning of the derivative becomes clear - the calculation of the angular coefficient of the tangent.
Find the abscissa value of the tangent point, which is denoted by the letter “a”. If it coincides with a given tangent point, then "a" will be its x-coordinate. Determine the value functions f(a) by substituting into the equation functions abscissa value.
Determine the first derivative of the equation functions f’(x) and substitute the value of point “a” into it.
Take the general tangent equation, which is defined as y = f(a) = f (a)(x – a), and substitute the found values of a, f(a), f "(a) into it. As a result, the solution to the graph will be found and tangent.
Solve the problem in a different way if the given tangent point does not coincide with the tangent point. In this case, it is necessary to substitute “a” instead of numbers in the tangent equation. After this, instead of the letters “x” and “y”, substitute the value of the coordinates of the given point. Solve the resulting equation in which “a” is the unknown. Plug the resulting value into the tangent equation.
Write an equation for a tangent with the letter “a” if the problem statement specifies the equation functions and the equation of a parallel line relative to the desired tangent. After this we need the derivative functions, to the coordinate at point “a”. Substitute the appropriate value into the tangent equation and solve the function.
Equation of the tangent to the graph of a function
P. Romanov, T. Romanova,
Magnitogorsk,
Chelyabinsk region
Equation of the tangent to the graph of a function
The article was published with the support of the ITAKA+ Hotel Complex. When staying in the city of shipbuilders Severodvinsk, you will not encounter the problem of finding temporary housing. , on the website of the hotel complex “ITHAKA+” http://itakaplus.ru, you can easily and quickly rent an apartment in the city, for any period, with a daily payment.
On modern stage development of education, one of its main tasks is the formation of a creatively thinking personality. The ability for creativity in students can be developed only if they are systematically involved in the basics of research activities. The foundation for students to use their creative powers, abilities and talents is formed full-fledged knowledge and skills. In this regard, the problem of forming a system of basic knowledge and skills for each topic of the school mathematics course is of no small importance. At the same time, full-fledged skills should be the didactic goal not of individual tasks, but of a carefully thought-out system of them. In the broadest sense, a system is understood as a set of interconnected interacting elements that have integrity and a stable structure.
Let's consider a technique for teaching students how to write an equation for a tangent to the graph of a function. Essentially, all problems of finding the tangent equation come down to the need to select from a set (bundle, family) of lines those that satisfy a certain requirement - they are tangent to the graph of a certain function. In this case, the set of lines from which selection is carried out can be specified in two ways:
a) a point lying on the xOy plane (central pencil of lines);
b) angular coefficient (parallel beam of straight lines).
In this regard, when studying the topic “Tangent to the graph of a function” in order to isolate the elements of the system, we identified two types of problems:
1) problems on a tangent given by the point through which it passes;
2) problems on a tangent given by its slope.
Training in solving tangent problems was carried out using the algorithm proposed by A.G. Mordkovich. Its fundamental difference from the already known ones is that the abscissa of the tangent point is denoted by the letter a (instead of x0), and therefore the tangent equation takes the form
y = f(a) + f "(a)(x – a)
(compare with y = f(x 0) + f "(x 0)(x – x 0)). This methodological technique, in our opinion, allows students to quickly and easily understand where the coordinates of the current point are written in the general tangent equation, and where are the points of contact.
Algorithm for composing the tangent equation to the graph of the function y = f(x)
1. Designate the abscissa of the tangent point with the letter a.
2. Find f(a).
3. Find f "(x) and f "(a).
4. Substitute the found numbers a, f(a), f "(a) into the general tangent equation y = f(a) = f "(a)(x – a).
This algorithm can be compiled on the basis of students’ independent identification of operations and the sequence of their implementation.
Practice has shown that the sequential solution of each of the key problems using an algorithm allows you to develop the skills of writing the equation of a tangent to the graph of a function in stages, and the steps of the algorithm serve as reference points for actions. This approach corresponds to the theory of the gradual formation of mental actions developed by P.Ya. Galperin and N.F. Talyzina.
In the first type of tasks, two key tasks were identified:
- the tangent passes through a point lying on the curve (problem 1);
- the tangent passes through a point not lying on the curve (problem 2).
Task 1. Write an equation for the tangent to the graph of the function 
at point M(3; – 2).
Solution. Point M(3; – 2) is a tangent point, since
1. a = 3 – abscissa of the tangent point.
2. f(3) = – 2.
3. f "(x) = x 2 – 4, f "(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – tangent equation.
Problem 2. Write the equations of all tangents to the graph of the function y = – x 2 – 4x + 2 passing through the point M(– 3; 6).
Solution. Point M(– 3; 6) is not a tangent point, since f(– 3) 6 (Fig. 2).
2. f(a) = – a 2 – 4a + 2.
3. f "(x) = – 2x – 4, f "(a) = – 2a – 4.
4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – tangent equation.
The tangent passes through the point M(– 3; 6), therefore, its coordinates satisfy the tangent equation.
6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a),
a 2 + 6a + 8 = 0^ a 1 = – 4, a 2 = – 2.
If a = – 4, then the tangent equation is y = 4x + 18.
If a = – 2, then the tangent equation has the form y = 6.
In the second type, the key tasks will be the following:
- the tangent is parallel to some line (problem 3);
- the tangent passes at a certain angle to the given line (problem 4).
Problem 3. Write the equations of all tangents to the graph of the function y = x 3 – 3x 2 + 3, parallel to the line y = 9x + 1.
Solution.
1. a – abscissa of the tangent point.
2. f(a) = a 3 – 3a 2 + 3.
3. f "(x) = 3x 2 – 6x, f "(a) = 3a 2 – 6a.
But, on the other hand, f "(a) = 9 (parallelism condition). This means that we need to solve the equation 3a 2 – 6a = 9. Its roots are a = – 1, a = 3 (Fig. 3).
4. 1) a = – 1;
2) f(– 1) = – 1;
3) f "(– 1) = 9;
4) y = – 1 + 9(x + 1);
y = 9x + 8 – tangent equation;
1) a = 3;
2) f(3) = 3;
3) f "(3) = 9;
4) y = 3 + 9(x – 3);
y = 9x – 24 – tangent equation.
Problem 4. Write the equation of the tangent to the graph of the function y = 0.5x 2 – 3x + 1, passing at an angle of 45° to the straight line y = 0 (Fig. 4).
Solution. From the condition f "(a) = tan 45° we find a: a – 3 = 1^a = 4.
1. a = 4 – abscissa of the tangent point.
2. f(4) = 8 – 12 + 1 = – 3.
3. f "(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4).
y = x – 7 – tangent equation.
It is easy to show that the solution to any other problem comes down to solving one or more key problems. Consider the following two problems as an example.
1. Write the equations of the tangents to the parabola y = 2x 2 – 5x – 2, if the tangents intersect at right angles and one of them touches the parabola at the point with abscissa 3 (Fig. 5).
Solution. Since the abscissa of the tangent point is given, the first part of the solution is reduced to key problem 1.
1. a = 3 – abscissa of the point of tangency of one of the sides of the right angle.
2. f(3) = 1.
3. f "(x) = 4x – 5, f "(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – equation of the first tangent.
Let a – angle of inclination of the first tangent. Since the tangents are perpendicular, then is the angle of inclination of the second tangent. From the equation y = 7x – 20 of the first tangent we have tg a = 7. Let's find
This means that the slope of the second tangent is equal to .
The further solution comes down to key task 3.
Let B(c; f(c)) be the point of tangency of the second line, then
1. – abscissa of the second point of tangency.
2.
3.
4.– equation of the second tangent.
Note. The angular coefficient of the tangent can be found more easily if students know the ratio of the coefficients of perpendicular lines k 1 k 2 = – 1.
2. Write the equations of all common tangents to the graphs of functions
Solution. The task comes down to finding the abscissa of the tangent points of common tangents, that is, solving key problem 1 in general form, drawing up a system of equations and then solving it (Fig. 6).
1. Let a be the abscissa of the tangent point lying on the graph of the function y = x 2 + x + 1.
2. f(a) = a 2 + a + 1.
3. f "(a) = 2a + 1.
4. y = a 2 + a + 1 + (2a + 1)(x – a) = (2a + 1)x + 1 – a 2 .
1. Let c be the abscissa of the tangent point lying on the graph of the function
2.
3. f "(c) = c.
4.
Since tangents are general, then
So y = x + 1 and y = – 3x – 3 are common tangents.
The main goal of the considered tasks is to prepare students to independently recognize the type of key problem when solving more complex problems that require certain research skills (the ability to analyze, compare, generalize, put forward a hypothesis, etc.). Such tasks include any task in which the key task is included as a component. Let us consider as an example the problem (inverse to Problem 1) of finding a function from the family of its tangents.
3. For what b and c are the lines y = x and y = – 2x tangent to the graph of the function y = x 2 + bx + c?
Solution.
Let t be the abscissa of the point of tangency of the straight line y = x with the parabola y = x 2 + bx + c; p is the abscissa of the point of tangency of the straight line y = – 2x with the parabola y = x 2 + bx + c. Then the tangent equation y = x will take the form y = (2t + b)x + c – t 2 , and the tangent equation y = – 2x will take the form y = (2p + b)x + c – p 2 .
Let's compose and solve a system of equations
Answer: 
Problems to solve independently
1. Write the equations of the tangents drawn to the graph of the function y = 2x 2 – 4x + 3 at the points of intersection of the graph with the line y = x + 3.
Answer: y = – 4x + 3, y = 6x – 9.5.
2. For what values of a does the tangent drawn to the graph of the function y = x 2 – ax at the point of the graph with the abscissa x 0 = 1 pass through the point M(2; 3)?
Answer: a = 0.5.
3. For what values of p does the straight line y = px – 5 touch the curve y = 3x 2 – 4x – 2?
Answer: p 1 = – 10, p 2 = 2.
4. Find all common points of the graph of the function y = 3x – x 3 and the tangent drawn to this graph through the point P(0; 16).
Answer: A(2; – 2), B(– 4; 52).
5. Find the shortest distance between the parabola y = x 2 + 6x + 10 and the straight line
Answer:
6. On the curve y = x 2 – x + 1, find the point at which the tangent to the graph is parallel to the straight line y – 3x + 1 = 0.
Answer: M(2; 3).
7. Write the equation of the tangent to the graph of the function y = x 2 + 2x – | 4x |, which touches it at two points. Make a drawing.
Answer: y = 2x – 4.
8. Prove that the line y = 2x – 1 does not intersect the curve y = x 4 + 3x 2 + 2x. Find the distance between their closest points.
Answer:
9. On the parabola y = x 2, two points are taken with abscissas x 1 = 1, x 2 = 3. A secant is drawn through these points. At what point of the parabola will the tangent to it be parallel to the secant? Write the secant and tangent equations.
Answer: y = 4x – 3 – secant equation; y = 4x – 4 – tangent equation.
10. Find the angle q between the tangents to the graph of the function y = x 3 – 4x 2 + 3x + 1, drawn at the points with abscissas 0 and 1.
Answer: q = 45°.
11. At what points does the tangent to the graph of the function form an angle of 135° with the Ox axis?
Answer: A(0; – 1), B(4; 3).
12. At point A(1; 8) to the curve 
a tangent is drawn. Find the length of the tangent segment between the coordinate axes.
Answer:
13. Write the equation of all common tangents to the graphs of the functions y = x 2 – x + 1 and y = 2x 2 – x + 0.5.
Answer: y = – 3x and y = x.
14. Find the distance between the tangents to the graph of the function 
parallel to the x-axis.
Answer:
15. Determine at what angles the parabola y = x 2 + 2x – 8 intersects the x-axis.
Answer: q 1 = arctan 6, q 2 = arctan (– 6).
16. Function graph 
find all points, the tangent at each of which to this graph intersects the positive semi-axes of coordinates, cutting off equal segments from them.
Answer: A(– 3; 11).
17. The line y = 2x + 7 and the parabola y = x 2 – 1 intersect at points M and N. Find the point K of intersection of the lines tangent to the parabola at points M and N.
Answer: K(1; – 9).
18. For what values of b is the line y = 9x + b tangent to the graph of the function y = x 3 – 3x + 15?
Answer: – 1; 31.
19. For what values of k does the straight line y = kx – 10 have only one common point with the graph of the function y = 2x 2 + 3x – 2? For the found values of k, determine the coordinates of the point.
Answer: k 1 = – 5, A(– 2; 0); k 2 = 11, B(2; 12).
20. For what values of b does the tangent drawn to the graph of the function y = bx 3 – 2x 2 – 4 at the point with the abscissa x 0 = 2 pass through the point M(1; 8)?
Answer: b = – 3.
21. A parabola with a vertex on the Ox axis touches the line passing through points A(1; 2) and B(2; 4) at point B. Find the equation of the parabola.
Answer: 
22. At what value of the coefficient k does the parabola y = x 2 + kx + 1 touch the Ox axis?
Answer: k = d 2.
23. Find the angles between the straight line y = x + 2 and the curve y = 2x 2 + 4x – 3.
29. Find the distance between the tangents to the graph of the function and the generators with the positive direction of the Ox axis at an angle of 45°.
Answer:
30. Find the locus of the vertices of all parabolas of the form y = x 2 + ax + b tangent to the line y = 4x – 1.
Answer: straight line y = 4x + 3.
Literature
1. Zvavich L.I., Shlyapochnik L.Ya., Chinkina M.V. Algebra and beginnings of analysis: 3600 problems for schoolchildren and those entering universities. – M., Bustard, 1999.
2. Mordkovich A. Seminar four for young teachers. Topic: Derivative Applications. – M., “Mathematics”, No. 21/94.
3. Formation of knowledge and skills based on the theory of gradual assimilation of mental actions. / Ed. P.Ya. Galperina, N.F. Talyzina. – M., Moscow State University, 1968.
In this article we will analyze all types of problems to find
Let's remember geometric meaning of derivative: if a tangent is drawn to the graph of a function at a point, then the slope coefficient of the tangent ( equal to tangent angle between the tangent and the positive direction of the axis) is equal to the derivative of the function at the point.
Let's take an arbitrary point on the tangent with coordinates:
And consider a right triangle:
In this triangle 
From here 
This is the equation of the tangent drawn to the graph of the function at the point.
To write the tangent equation, we only need to know the equation of the function and the point at which the tangent is drawn. Then we can find and .
There are three main types of tangent equation problems.
1. Given a point of contact
2. The tangent slope coefficient is given, that is, the value of the derivative of the function at the point.
3. Given are the coordinates of the point through which the tangent is drawn, but which is not the point of tangency.
Let's look at each type of task.
1 . Write the equation of the tangent to the graph of the function 
at the point .
.
b) Find the value of the derivative at point . First let's find the derivative of the function
Let's substitute the found values into the tangent equation:
Let's open the brackets on the right side of the equation. We get:
Answer: .
2. Find the abscissa of the points at which the functions are tangent to the graph 
parallel to the x-axis.
If the tangent is parallel to the x-axis, therefore the angle between the tangent and the positive direction of the axis is zero, therefore the tangent of the tangent angle is zero. This means that the value of the derivative of the function at the points of contact is zero.
a) Find the derivative of the function .
b) Let’s equate the derivative to zero and find the values in which the tangent is parallel to the axis:
Equating each factor to zero, we get:
Answer: 0;3;5
3. Write equations for tangents to the graph of a function , parallel straight .
A tangent is parallel to a line. The slope of this line is -1. Since the tangent is parallel to this line, therefore, the slope of the tangent is also -1. That is we know the slope of the tangent, and, thereby, derivative value at the point of tangency.
This is the second type of problem to find the tangent equation.
So, we are given the function and the value of the derivative at the point of tangency.
a) Find the points at which the derivative of the function is equal to -1.
First, let's find the derivative equation.
Let's equate the derivative to the number -1.
Let's find the value of the function at the point.
(by condition)
.
b) Find the equation of the tangent to the graph of the function at point .
Let's find the value of the function at the point.
(by condition).
Let's substitute these values into the tangent equation:
.
Answer:
4 . Write the equation of the tangent to the curve , passing through a point
First, let's check if the point is a tangent point. If a point is a tangent point, then it belongs to the graph of the function, and its coordinates must satisfy the equation of the function. Let's substitute the coordinates of the point into the equation of the function.
Title="1sqrt(8-3^2)">. Мы получили под корнем !} a negative number, the equality is not true, and the point does not belong to the graph of the function and is not a point of contact.
This is the last type of problem to find the tangent equation. First thing we need to find the abscissa of the tangent point.
Let's find the value.
Let be the point of contact. The point belongs to the tangent to the graph of the function. If we substitute the coordinates of this point into the tangent equation, we get the correct equality:
.
The value of the function at a point is 
.
Let's find the value of the derivative of the function at the point.
First, let's find the derivative of the function. This .
The derivative at a point is equal to 
.
Let's substitute the expressions for and into the tangent equation. We get the equation for:
Let's solve this equation.
Reduce the numerator and denominator of the fraction by 2:
Let's bring the right side of the equation to a common denominator. We get:
Let's simplify the numerator of the fraction and multiply both sides by - this expression is strictly greater than zero.
We get the equation
Let's solve it. To do this, let's square both parts and move on to the system.
Title="delim(lbrace)(matrix(2)(1)((64-48(x_0)+9(x_0)^2=8-(x_0)^2) (8-3x_0>=0 ) ))( )">!}
Let's solve the first equation.
Let's decide quadratic equation, we get
The second root does not satisfy the condition title="8-3x_0>=0">, следовательно, у нас только одна точка касания и её абсцисса равна .!}
Let's write the equation of the tangent to the curve at the point. To do this, substitute the value into the equation 
- We already recorded it.
Answer:
.
Consider the following figure:
It depicts a certain function y = f(x), which is differentiable at point a. Point M with coordinates (a; f(a)) is marked. A secant MR is drawn through an arbitrary point P(a + ∆x; f(a + ∆x)) of the graph.
If now point P is shifted along the graph to point M, then straight line MR will rotate around point M. In this case, ∆x will tend to zero. From here we can formulate the definition of a tangent to the graph of a function.
Tangent to the graph of a function
The tangent to the graph of a function is the limiting position of the secant as the increment of the argument tends to zero. It should be understood that the existence of the derivative of the function f at the point x0 means that at this point of the graph there is tangent to him.
In this case, the angular coefficient of the tangent will be equal to the derivative of this function at this point f’(x0). This is the geometric meaning of the derivative. The tangent to the graph of a function f differentiable at point x0 is a certain straight line passing through the point (x0;f(x0)) and having an angular coefficient f’(x0).
Tangent equation
Let's try to obtain the equation of the tangent to the graph of some function f at point A(x0; f(x0)). The equation of a straight line with slope k has next view:
Since our slope coefficient is equal to the derivative f’(x0), then the equation will take the following form: y = f’(x0)*x + b.
Now let's calculate the value of b. To do this, we use the fact that the function passes through point A.
f(x0) = f’(x0)*x0 + b, from here we express b and get b = f(x0) - f’(x0)*x0.
We substitute the resulting value into the tangent equation:
y = f’(x0)*x + b = f’(x0)*x + f(x0) - f’(x0)*x0 = f(x0) + f’(x0)*(x - x0).
y = f(x0) + f’(x0)*(x - x0).
Consider the following example: find the equation of the tangent to the graph of the function f(x) = x 3 - 2*x 2 + 1 at point x = 2.
2. f(x0) = f(2) = 2 2 - 2*2 2 + 1 = 1.
3. f’(x) = 3*x 2 - 4*x.
4. f’(x0) = f’(2) = 3*2 2 - 4*2 = 4.
5. Substitute the obtained values into the tangent formula, we get: y = 1 + 4*(x - 2). Opening the brackets and bringing similar terms we get: y = 4*x - 7.
Answer: y = 4*x - 7.
General scheme for composing the tangent equation to the graph of the function y = f(x):
1. Determine x0.
2. Calculate f(x0).
3. Calculate f’(x)
A tangent is a straight line , which touches the graph of the function at one point and all points of which are at the shortest distance from the graph of the function. Therefore, the tangent passes tangent to the graph of the function at a certain angle, and several tangents at different angles cannot pass through the point of tangency. Tangent equations and normal equations to the graph of a function are constructed using the derivative.
The tangent equation is derived from the line equation .
Let us derive the equation of the tangent, and then the equation of the normal to the graph of the function.
y = kx + b .
In him k- angular coefficient.
From here we get the following entry:
y - y 0 = k(x - x 0 ) .
Derivative value f "(x 0 ) functions y = f(x) at the point x0 equal to the slope k= tg φ tangent to the graph of a function drawn through a point M0 (x 0 , y 0 ) , Where y0 = f(x 0 ) . This is geometric meaning of derivative .
Thus, we can replace k on f "(x 0 ) and get the following equation of the tangent to the graph of a function :
y - y 0 = f "(x 0 )(x - x 0 ) .
In problems involving composing the equation of a tangent to the graph of a function (and we will move on to them soon), it is required to reduce the equation obtained from the above formula to equation of a straight line in general form. To do this, you need to transfer all letters and numbers to left side equation, and leave zero on the right side.
Now about the normal equation. Normal - this is a straight line passing through the point of tangency to the graph of the function perpendicular to the tangent. Normal equation :
(x - x 0 ) + f "(x 0 )(y - y 0 ) = 0
To warm up, you are asked to solve the first example yourself, and then look at the solution. There is every reason to hope that this task will not be a “cold shower” for our readers.
Example 0. Create a tangent equation and a normal equation for the graph of a function at a point M (1, 1) .
Example 1. Write a tangent equation and a normal equation for the graph of a function 
, if the abscissa is tangent .
Let's find the derivative of the function:
Now we have everything that needs to be substituted into the entry given in the theoretical help to get the tangent equation. We get
In this example, we were lucky: the slope turned out to be zero, so we separately reduce the equation to general appearance wasn't needed. Now we can create the normal equation:
In the figure below: graph of a function in burgundy color, tangent Green colour, orange normal.
The next example is also not complicated: the function, as in the previous one, is also a polynomial, but the slope will not be equal to zero, so one more step will be added - bringing the equation to a general form.
Example 2.
Solution. Let's find the ordinate of the tangent point:
Let's find the derivative of the function:
.
Let's find the value of the derivative at the point of tangency, that is, the slope of the tangent:
We substitute all the obtained data into the “blank formula” and get the tangent equation:
We bring the equation to its general form (we collect all letters and numbers other than zero on the left side, and leave zero on the right):
We compose the normal equation:
Example 3. Write the equation of the tangent and the equation of the normal to the graph of the function if the abscissa is the point of tangency.
Solution. Let's find the ordinate of the tangent point:
Let's find the derivative of the function:
.
Let's find the value of the derivative at the point of tangency, that is, the slope of the tangent:
.
We find the tangent equation:
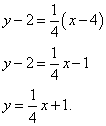
Before bringing the equation to its general form, you need to “comb it” a little: multiply term by term by 4. We do this and bring the equation to its general form:
We compose the normal equation:
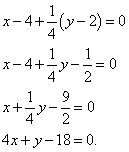
Example 4. Write the equation of the tangent and the equation of the normal to the graph of the function if the abscissa is the point of tangency.
Solution. Let's find the ordinate of the tangent point:
.
Let's find the derivative of the function:
Let's find the value of the derivative at the point of tangency, that is, the slope of the tangent:
.
We get the tangent equation:
We bring the equation to its general form:
We compose the normal equation:
A common mistake when writing tangent and normal equations is not to notice that the function given in the example is complex and to calculate its derivative as the derivative of a simple function. The following examples are already from complex functions(the corresponding lesson will open in a new window).
Example 5. Write the equation of the tangent and the equation of the normal to the graph of the function if the abscissa is the point of tangency.
Solution. Let's find the ordinate of the tangent point:
Attention! This function is complex, since the tangent argument (2 x) is itself a function. Therefore, we find the derivative of a function as the derivative of a complex function.
Loading...