პერიოდული წილადის წარმოდგენა საერთო წილადში. ათწილადები, განმარტებები, აღნიშვნა, მაგალითები, მოქმედებები ათწილადებით

ეს სტატია ეხება ათწილადები. აქ გავიგებთ წილადი რიცხვების ათობითი აღნიშვნას, გავაცნობთ ათობითი წილადის ცნებას და მოვიყვანთ ათობითი წილადების მაგალითებს. შემდეგ ვისაუბრებთ ათობითი წილადების ციფრებზე და დავასახელებთ ციფრების სახელებს. ამის შემდეგ ყურადღებას გავამახვილებთ უსასრულო ათობითი წილადებზე, ვისაუბროთ პერიოდულ და არაპერიოდულ წილადებზე. ქვემოთ ჩამოვთვლით ძირითად მოქმედებებს ათწილადები. დასასრულს, მოდით დავადგინოთ ათობითი წილადების პოზიცია კოორდინატულ სხივზე.

გვერდის ნავიგაცია.

წილადი რიცხვის ათწილადი აღნიშვნა

ათწილადების კითხვა

მოდით ვთქვათ რამდენიმე სიტყვა ათწილადის წილადების წაკითხვის წესებზე.

ათწილადი წილადები, რომლებიც შეესაბამება სწორ ჩვეულებრივ წილადებს, იკითხება ისევე, როგორც ეს ჩვეულებრივი წილადები, ჯერ ემატება მხოლოდ "ნულოვანი მთელი რიცხვი". მაგალითად, ათობითი წილადი 0.12 შეესაბამება საერთო წილადს 12/100 (წაიკითხეთ „თორმეტი ასეული“), შესაბამისად, 0.12 იკითხება როგორც „ნულოვანი წერტილი თორმეტი მეასედი“.

ათწილადი წილადები, რომლებიც შეესაბამება შერეულ რიცხვებს, იკითხება ზუსტად ისე, როგორც ეს შერეული რიცხვები. მაგალითად, ათობითი წილადი 56.002 შეესაბამება შერეულ რიცხვს, ამიტომ ათწილადი 56.002 იკითხება როგორც „ორმოცდათექვსმეტი წერტილი ორი მეათასედი“.

ადგილები ათწილადებში

ათობითი წილადების წერისას, ასევე წერისას ნატურალური რიცხვები, თითოეული ციფრის მნიშვნელობა დამოკიდებულია მის პოზიციაზე. მართლაც, რიცხვი 3 ათობითი წილადში 0.3 ნიშნავს სამ მეათედს, ათწილადში 0.0003 - სამ ათი მეათასედს, ხოლო ათობითი წილადში 30000.152 - სამ ათეულ ათასს. ასე რომ, ჩვენ შეგვიძლია ვისაუბროთ ათობითი ადგილები, ასევე ნატურალური რიცხვების ციფრების შესახებ.

ათწილადის წილადის ციფრების სახელები ათწილადამდე სრულად ემთხვევა ნატურალურ რიცხვებში მოცემული ციფრების სახელებს. ხოლო ათობითი ადგილების სახელები ათწილადის შემდეგ ჩანს შემდეგი ცხრილიდან.

მაგალითად, ათობითი წილადში 37.051, ციფრი 3 არის ათეულების ადგილზე, 7 არის ერთეულების ადგილზე, 0 არის მეათედებში, 5 არის მეასედებში და 1 არის მეათასედებში.

ათობითი წილადებში ადგილები ასევე განსხვავდება უპირატესობით. თუ ათობითი წილადის ჩაწერისას გადავალთ ციფრიდან ციფრზე მარცხნიდან მარჯვნივ, მაშინ გადავალთ უფროსებირომ უმცროსი წოდებები. მაგალითად, ასეულების ადგილი უფრო ძველია, ვიდრე მეათე ადგილი, ხოლო მილიონი ადგილი უფრო დაბალია, ვიდრე მეათე ადგილი. მოცემულ საბოლოო ათობითი წილადში შეგვიძლია ვისაუბროთ მთავარ და მცირე ციფრებზე. მაგალითად, ათობითი წილადში 604.9387 უფროსი (უმაღლესი)ადგილი არის ასობით ადგილი და უმცროსი (ყველაზე დაბალი)- ათიათასიანი ციფრი.

ათობითი წილადებისთვის, ხდება ციფრებად გაფართოება. ეს ნატურალური რიცხვების ციფრებად გაფართოების მსგავსია. მაგალითად, 45,6072 ათწილადების გაფართოება შემდეგია: 45,6072=40+5+0,6+0,007+0,0002. ხოლო ათობითი წილადის ციფრებად დაშლის შედეგად შეკრების თვისებები საშუალებას გაძლევთ გადახვიდეთ ამ ათობითი წილადის სხვა წარმოდგენებზე, მაგალითად, 45.6072=45+0.6072, ან 45.6072=40.6+5.007+0.0002, ან 45.65.0072= . 0.6.

ბოლო ათწილადები

ამ დრომდე ჩვენ მხოლოდ ათწილად წილადებზე ვისაუბრეთ, რომელთა აღნიშვნაში არის სასრული რიცხვი ათწილადის შემდეგ. ასეთ წილადებს სასრულ ათწილადებს უწოდებენ.

განმარტება.

ბოლო ათწილადები- ეს არის ათობითი წილადები, რომელთა ჩანაწერები შეიცავს სიმბოლოების (ციფრების) სასრულ რაოდენობას.

აქ მოცემულია საბოლოო ათობითი წილადების რამდენიმე მაგალითი: 0.317, 3.5, 51.1020304958, 230,032.45.

თუმცა, ყველა წილადი არ შეიძლება იყოს წარმოდგენილი საბოლოო ათწილადად. მაგალითად, წილადი 5/13 არ შეიძლება შეიცვალოს ტოლი წილადით ერთ-ერთი მნიშვნელით 10, 100, ..., შესაბამისად, ვერ გადაიქცევა საბოლოო ათობითი წილადად. ამის შესახებ დაწვრილებით ვისაუბრებთ თეორიის განყოფილებაში, ჩვეულებრივი წილადების ათწილადებად გადაქცევით.

უსასრულო წილადები: პერიოდული წილადები და არაპერიოდული წილადები

ათობითი წერტილის შემდეგ ათობითი წილადის დაწერისას, შეგიძლიათ ვივარაუდოთ უსასრულო რაოდენობის ციფრების შესაძლებლობა. ამ შემთხვევაში ჩვენ განვიხილავთ ეგრეთ წოდებულ უსასრულო ათობითი წილადებს.

განმარტება.

უსასრულო ათწილადები- ეს არის ათობითი წილადები, რომლებიც შეიცავს უსასრულო რიცხვს.

გასაგებია, რომ ჩვენ არ შეგვიძლია ჩავწეროთ უსასრულო ათობითი წილადები სრული სახით, ამიტომ მათი ჩაწერისას ჩვენ შემოვიფარგლებით მხოლოდ გარკვეული სასრული რაოდენობის ციფრებით ათობითი წერტილის შემდეგ და ვაყენებთ ელიფსისს, რომელიც მიუთითებს ციფრების უსასრულოდ უწყვეტ მიმდევრობას. აქ მოცემულია უსასრულო ათობითი წილადების რამდენიმე მაგალითი: 0.143940932…, 3.1415935432…, 153.02003004005…, 2.111111111…, 69.74152152152….

თუ კარგად დააკვირდებით ბოლო ორ უსასრულო ათობითი წილადს, მაშინ წილადში 2.111111111... უსასრულოდ განმეორებადი რიცხვი 1 აშკარად ჩანს, ხოლო წილადში 69.74152152152... მესამე ათწილადიდან დაწყებული რიცხვების განმეორებითი ჯგუფი. 1, 5 და 2 აშკარად ჩანს. ასეთ უსასრულო ათობითი წილადებს პერიოდული ეწოდება.

განმარტება.

პერიოდული ათწილადები(ან უბრალოდ პერიოდული წილადები) არის უსასრულო ათობითი წილადები, რომელთა ჩანაწერში, გარკვეული ათწილადიდან დაწყებული, უსასრულოდ მეორდება რაღაც რიცხვი ან რიცხვების ჯგუფი, რომელიც ე.წ. წილადის პერიოდი.

მაგალითად, პერიოდული წილადის პერიოდი 2.111111111... არის ციფრი 1, ხოლო წილადის პერიოდი 69.74152152152... არის 152 ფორმის ციფრთა ჯგუფი.

უსასრულო პერიოდული ათობითი წილადებისთვის მიღებულია სპეციალური ფორმაჩანაწერები. მოკლედ, შევთანხმდით, რომ ჩავწეროთ პერიოდი ერთხელ, ჩავსვათ იგი ფრჩხილებში. მაგალითად, პერიოდული წილადი 2.111111111... იწერება როგორც 2,(1) , ხოლო პერიოდული წილადი 69.74152152152... იწერება როგორც 69.74(152) .

აღსანიშნავია, რომ იგივე პერიოდული ათობითი წილადისთვის შეგიძლიათ მიუთითოთ სხვადასხვა პერიოდები. მაგალითად, პერიოდული ათობითი წილადი 0,73333... შეიძლება ჩაითვალოს წილადად 0,7(3) 3-იანი პერიოდით, ასევე წილადად 0,7(33) 33-იანი პერიოდით და ასე შემდეგ 0,7(333), 0,7 (3333), ... ასევე შეგიძლიათ შეხედოთ პერიოდულ წილადს 0,73333 ... ასე: 0,733(3), ან ასე 0,73(333) და ა.შ. აქ, გაურკვევლობისა და შეუსაბამობების თავიდან აცილების მიზნით, ჩვენ ვეთანხმებით, რომ ათწილადი წილადის პერიოდად მივიჩნიოთ უმოკლესი ყველა შესაძლო მიმდევრობით რიცხვების განმეორებით და დაწყებული უახლოესი პოზიციიდან ათწილადამდე. ანუ ათწილადის 0,73333... პერიოდი ჩაითვლება ერთი ციფრი 3-ის მიმდევრობით, ხოლო პერიოდულობა იწყება ათწილადის შემდეგ მეორე პოზიციიდან, ანუ 0,73333...=0,7(3). კიდევ ერთი მაგალითი: პერიოდულ წილადს 4.7412121212... აქვს პერიოდი 12, პერიოდულობა იწყება ათობითი წერტილის შემდეგ მესამე ციფრიდან, ანუ 4.7412121212...=4.74(12).

უსასრულო ათობითი პერიოდული წილადები მიიღება ათწილადად გადაყვანისას ჩვეულებრივი წილადები, რომლის მნიშვნელები შეიცავს პირველ ფაქტორებს, გარდა 2-ისა და 5-ისა.

აქ უნდა აღინიშნოს პერიოდული წილადები 9-იანი პერიოდით. მოვიყვანოთ ასეთი წილადების მაგალითები: 6.43(9) , 27,(9) . ეს წილადები არის კიდევ ერთი აღნიშვნა პერიოდული წილადებისთვის 0 პერიოდით და ისინი ჩვეულებრივ იცვლება პერიოდული წილადებით 0 პერიოდით. ამისათვის პერიოდი 9 იცვლება 0 პერიოდით, ხოლო შემდეგი უმაღლესი ციფრის მნიშვნელობა იზრდება ერთით. მაგალითად, წილადი 7.24(9) ფორმის 9 პერიოდით იცვლება პერიოდული წილადით 7.25(0) ფორმის 0 წერტილით ან ტოლი საბოლოო ათობითი წილადი 7.25. კიდევ ერთი მაგალითი: 4,(9)=5,(0)=5. მე-9 პერიოდის მქონე წილადის და 0 პერიოდის შესაბამისი წილადის ტოლობა ადვილად დგინდება ამ ათობითი წილადების ტოლი ჩვეულებრივი წილადებით ჩანაცვლების შემდეგ.

და ბოლოს, მოდით უფრო ახლოს მივხედოთ უსასრულო ათობითი წილადებს, რომლებიც არ შეიცავს უსასრულოდ განმეორებადი ციფრების თანმიმდევრობას. მათ უწოდებენ არა პერიოდულს.

განმარტება.

არაგანმეორებადი ათწილადები(ან უბრალოდ არაპერიოდული წილადები) არის უსასრულო ათობითი წილადები, რომლებსაც არ აქვთ წერტილი.

ზოგჯერ არაპერიოდულ წილადებს აქვთ პერიოდული წილადების მსგავსი ფორმა, მაგალითად, 8.02002000200002... არის არაპერიოდული წილადი. ამ შემთხვევაში განსაკუთრებული სიფრთხილით უნდა შეამჩნიოთ განსხვავება.

გაითვალისწინეთ, რომ არაპერიოდული წილადები არ გარდაიქმნება ჩვეულებრივ წილადებად; უსასრულო არაპერიოდული ათობითი წილადები წარმოადგენს ირაციონალურ რიცხვებს.

ოპერაციები ათწილადებით

ათობითი წილადების ერთ-ერთი ოპერაცია არის შედარება და ასევე განისაზღვრება ოთხი ძირითადი არითმეტიკული ფუნქცია. ოპერაციები ათწილადებით: შეკრება, გამოკლება, გამრავლება და გაყოფა. განვიხილოთ ცალ-ცალკე თითოეული მოქმედება ათობითი წილადებით.

ათწილადების შედარებაარსებითად ეფუძნება შედარებული ათობითი წილადების შესაბამისი ჩვეულებრივი წილადების შედარებას. თუმცა, ათობითი წილადების ჩვეულებრივ წილადებად გადაქცევა საკმაოდ შრომატევადი პროცესია და უსასრულო არაპერიოდული წილადები არ შეიძლება იყოს წარმოდგენილი როგორც ჩვეულებრივი წილადი, ამიტომ მოსახერხებელია ათწილადების ადგილობრივი შედარება. ათობითი წილადების ადგილის მიხედვით შედარება ნატურალური რიცხვების შედარების მსგავსია. უფრო დეტალური ინფორმაციისთვის გირჩევთ სტატიის შესწავლას: ათობითი წილადების შედარება, წესები, მაგალითები, ამონახსნები.

მოდით გადავიდეთ შემდეგი მოქმედება - ათწილადების გამრავლება. სასრული ათობითი წილადების გამრავლება ხორციელდება ათწილადების გამოკლების მსგავსად, წესები, მაგალითები, ნატურალური რიცხვების სვეტით გამრავლების ამონახსნები. პერიოდული წილადების შემთხვევაში გამრავლება შეიძლება შემცირდეს ჩვეულებრივი წილადების გამრავლებამდე. თავის მხრივ, უსასრულო არაპერიოდული ათობითი წილადების გამრავლება მათი დამრგვალების შემდეგ მცირდება სასრულ ათობითი წილადების გამრავლებამდე. სტატიაში მასალის შემდგომი შესწავლისთვის გირჩევთ: ათობითი წილადების გამრავლება, წესები, მაგალითები, ამონახსნები.

ათწილადები კოორდინატულ სხივზე

წერტილებსა და ათწილადებს შორის არის ერთი-ერთზე შესაბამისობა.

მოდით გავარკვიოთ, როგორ არის აგებული წერტილები კოორდინატულ სხივზე, რომლებიც შეესაბამება მოცემულ ათობითი წილადს.

ჩვენ შეგვიძლია შევცვალოთ სასრული ათობითი წილადები და უსასრულო პერიოდული ათობითი წილადები თანაბარი ჩვეულებრივი წილადებით და შემდეგ ავაშენოთ შესაბამისი ჩვეულებრივი წილადები კოორდინატულ სხივზე. მაგალითად, ათობითი წილადი 1.4 შეესაბამება საერთო წილადს 14/10, ამიტომ წერტილი 1.4 კოორდინატით ამოღებულია საწყისიდან დადებითი მიმართულებით 14 სეგმენტით, რომელიც ტოლია ერთეულის სეგმენტის მეათედს.

ათწილადი წილადები შეიძლება აღინიშნოს კოორდინატულ სხივზე, დაწყებული მოცემული ათობითი წილადის ციფრებად დაშლით. მაგალითად, უნდა ავაშენოთ წერტილი 16.3007 კოორდინატით, ვინაიდან 16.3007=16+0.3+0.0007, მაშინ ჩვენ შეგვიძლია მივიდეთ ამ პუნქტამდე კოორდინატების საწყისიდან 16 ერთეული სეგმენტის თანმიმდევრულად დაყენებით, 3 სეგმენტის, რომელთა სიგრძე უდრის მეათედს. ერთეულის და 7 სეგმენტი, რომელთა სიგრძე უდრის ერთეულის სეგმენტის ათიათასედს.

მშენებლობის ეს გზა ათობითი რიცხვებიკოორდინატთა სხივზე საშუალებას გაძლევთ მიუახლოვდეთ უსასრულო ათობითი წილადის შესაბამის წერტილს, როგორც გსურთ.

ზოგჯერ შესაძლებელია ზუსტად გამოსახოთ წერტილი, რომელიც შეესაბამება უსასრულო ათობითი წილადს. Მაგალითად, , მაშინ ეს უსასრულო ათობითი წილადი 1.41421... შეესაბამება კოორდინატთა სხივის წერტილს, რომელიც დაშორებულია კოორდინატების საწყისიდან კვადრატის დიაგონალის სიგრძით, გვერდითი 1 ერთეული სეგმენტით.

კოორდინატულ სხივზე მოცემული წერტილის შესაბამისი ათობითი წილადის მიღების საპირისპირო პროცესია ე.წ. სეგმენტის ათობითი გაზომვა. მოდით გავარკვიოთ, როგორ კეთდება.

დაე, ჩვენი ამოცანა იყოს საწყისიდან კოორდინატთა წრფის მოცემულ წერტილამდე მისვლა (ან უსასრულოდ მიახლოება, თუ მას ვერ მივაღწევთ). სეგმენტის ათობითი გაზომვით, ჩვენ შეგვიძლია თანმიმდევრულად გამოვყოთ საწყისიდან ნებისმიერი რაოდენობის ერთეული სეგმენტები, შემდეგ სეგმენტები, რომელთა სიგრძე უდრის მეათედი ერთეულის, შემდეგ სეგმენტები, რომელთა სიგრძე უდრის ერთეულის მეასედს და ა.შ. თითოეული სიგრძის სეგმენტების რაოდენობის ჩაწერით, ჩვენ ვიღებთ ათწილადს, რომელიც შეესაბამება კოორდინატთა სხივის მოცემულ წერტილს.

მაგალითად, ზემოთ მოცემულ ფიგურაში M წერტილამდე მისასვლელად, თქვენ უნდა გამოყოთ 1 ერთეული სეგმენტი და 4 სეგმენტი, რომელთა სიგრძე უდრის ერთეულის მეათედს. ამრიგად, M წერტილი შეესაბამება ათობითი წილადს 1.4.

ნათელია, რომ კოორდინატთა სხივის წერტილები, რომელთა მიღწევა შეუძლებელია ათობითი გაზომვის პროცესში, შეესაბამება უსასრულო ათობითი წილადებს.

ბიბლიოგრაფია.

• მათემატიკა: სახელმძღვანელო მე-5 კლასისთვის. ზოგადი განათლება ინსტიტუტები / ნ. ია. ვილენკინი, ვ. ი. ჟოხოვი, ა. ს. ჩესნოკოვი, ს.ი. შვარცბურდი. - 21-ე გამოცემა, წაშლილია. - M.: Mnemosyne, 2007. - 280 გვ.: ill. ISBN 5-346-00699-0.
• მათემატიკა.მე-6 კლასი: საგანმანათლებლო. ზოგადი განათლებისთვის დაწესებულებები / [ნ. ია ვილენკინი და სხვები]. - 22-ე გამოცემა, რევ. - მ.: მნემოსინე, 2008. - 288 გვ.: ილ. ISBN 978-5-346-00897-2.
• Ალგებრა:სახელმძღვანელო მე-8 კლასისთვის. ზოგადი განათლება ინსტიტუტები / [იუ. ნ. მაკარიჩევი, ნ.გ.მინდიუკი, კ.ი.ნეშკოვი, ს.ბ.სუვოროვა]; რედაქტორი S.A. თელიაკოვსკი. - მე-16 გამოცემა. - მ.: განათლება, 2008. - 271გვ. : ავად. - ISBN 978-5-09-019243-9.
• გუსევი V.A., Mordkovich A.G.მათემატიკა (სახელმძღვანელო ტექნიკურ სასწავლებლებში შესვლისთვის): პროკ. შემწეობა.- მ. უმაღლესი სკოლა, 1984.-351გვ., ილ.

როგორც ცნობილია, რაციონალური რიცხვების სიმრავლე (Q) მოიცავს მთელ რიცხვთა სიმრავლეს (Z), რომელიც თავის მხრივ მოიცავს ნატურალური რიცხვების სიმრავლეს (N). მთელი რიცხვების გარდა, რაციონალურ რიცხვებში შედის წილადები.

მაშინ რატომ განიხილება რაციონალური რიცხვების მთელი სიმრავლე ზოგჯერ უსასრულო პერიოდულ ათობითი წილადებად? მართლაც, წილადების გარდა, მათში ასევე შედის მთელი რიცხვები, ისევე როგორც არაპერიოდული წილადები.

ფაქტია, რომ ყველა მთელი რიცხვი, ისევე როგორც ნებისმიერი წილადი, შეიძლება წარმოდგენილი იყოს როგორც უსასრულო პერიოდული ათობითი წილადი. ანუ, ყველა რაციონალური რიცხვისთვის შეგიძლიათ გამოიყენოთ ერთი და იგივე ჩაწერის მეთოდი.

როგორ არის წარმოდგენილი უსასრულო პერიოდული ათწილადი? მასში ათწილადის შემდეგ რიცხვების განმეორებითი ჯგუფი მოთავსებულია ფრჩხილებში. მაგალითად, 1.56(12) არის წილადი, რომელშიც მეორდება რიცხვების ჯგუფი 12, ანუ წილადს აქვს მნიშვნელობა 1.561212121212... და ასე უსასრულოდ. რიცხვების განმეორებით ჯგუფს პერიოდს უწოდებენ.

თუმცა ამ ფორმით ნებისმიერი რიცხვი შეგვიძლია გამოვსახოთ, თუ მის პერიოდს მივიჩნევთ რიცხვად 0, რომელიც ასევე უსასრულოდ მეორდება. მაგალითად, რიცხვი 2 იგივეა, რაც 2.00000.... მაშასადამე, ის შეიძლება დაიწეროს როგორც უსასრულო პერიოდული წილადი, ანუ 2,(0).

იგივე შეიძლება გაკეთდეს ნებისმიერ სასრულ წილადთან. Მაგალითად:

0,125 = 0,1250000... = 0,125(0)

თუმცა, პრაქტიკაში ისინი არ იყენებენ სასრულ წილადის უსასრულო პერიოდულად გარდაქმნას. ამიტომ ისინი განასხვავებენ სასრულ წილადებს და უსასრულო პერიოდულებს. ამრიგად, უფრო სწორია იმის თქმა, რომ რაციონალური რიცხვები მოიცავს

• ყველა მთელი რიცხვი
• საბოლოო წილადები,
• უსასრულო პერიოდული წილადები.

ამავე დროს, უბრალოდ დაიმახსოვრეთ, რომ მთელი რიცხვები და სასრული წილადები თეორიულად წარმოდგენილია უსასრულო პერიოდული წილადების სახით.

მეორე მხრივ, ცნებები სასრული და უსასრულო წილადიგამოიყენება ათობითი წილადებისთვის. როდესაც საქმე ეხება წილადებს, სასრული და უსასრულო ათწილადები შეიძლება ცალსახად იყოს წარმოდგენილი წილადის სახით. ეს ნიშნავს, რომ ჩვეულებრივი წილადების თვალსაზრისით, პერიოდული და სასრული წილადები ერთი და იგივეა. გარდა ამისა, მთელი რიცხვები ასევე შეიძლება წარმოდგენილი იყოს წილადის სახით, წარმოვიდგინოთ, რომ ჩვენ ვყოფთ რიცხვს 1-ზე.

როგორ წარმოვიდგინოთ ათობითი უსასრულო პერიოდული წილადი ჩვეულებრივ წილადად? ყველაზე ხშირად გამოყენებული ალგორითმი მსგავსია:

1. შეამცირეთ წილადი ისე, რომ ათობითი წერტილის შემდეგ დარჩეს მხოლოდ წერტილი.
2. გაამრავლეთ უსასრულო პერიოდული წილადი 10-ზე ან 100-ზე ან ... ისე, რომ ათობითი წერტილი გადავიდეს მარჯვნივ ერთი წერტილით (ე.ი. ერთი წერტილი სრულდება მთელ ნაწილში).
3. გაუტოლეთ საწყისი წილადი (a) x ცვლადს და წილადი (b) მიღებული N რიცხვით Nx-ზე გამრავლებით.
4. გამოვაკლოთ x Nx-ს. b-ს ვაკლებ a. ანუ ისინი ქმნიან განტოლებას Nx – x = b – a.
5. განტოლების ამოხსნისას შედეგი არის ჩვეულებრივი წილადი.

უსასრულო პერიოდული ათობითი წილადის ჩვეულებრივ წილადად გადაქცევის მაგალითი:
x = 1.13333...
10x = 11.3333...
10x * 10 = 11.33333... * 10
100x = 113.3333...
100x – 10x = 113.3333... – 11.3333...
90x = 102
x =

რაციონალური რიცხვი m/n ათწილადის სახით დასაწერად, მრიცხველი უნდა გაყოთ მნიშვნელზე. ამ შემთხვევაში, კოეფიციენტი იწერება როგორც სასრული ან უსასრულო ათობითი წილადი.

Ჩაწერა მოცემული ნომერიროგორც ათობითი წილადი.

გამოსავალი. გაყავით თითოეული წილადის მრიცხველი სვეტად მისი მნიშვნელის მიხედვით: ა)გაყავით 6 25-ზე; ბ)გაყავით 2 3-ზე; V)გაყავით 1 2-ზე და შემდეგ დაამატეთ მიღებული წილადი - ამ შერეული რიცხვის მთელი რიცხვი.

შეუქცევადი ჩვეულებრივი წილადები, რომელთა მნიშვნელები არ შეიცავს მარტივ ფაქტორებს გარდა 2 და 5 , იწერება როგორც საბოლოო ათობითი წილადი.

IN მაგალითი 1როდესაც ა)მნიშვნელი 25=5·5; როდესაც V)მნიშვნელი არის 2, ამიტომ მივიღებთ საბოლოო ათწილადებს 0.24 და 1.5. Როდესაც ბ)მნიშვნელი არის 3, ამიტომ შედეგი არ შეიძლება ჩაიწეროს სასრულ ათწილადად.

შესაძლებელია თუ არა გრძელი გაყოფის გარეშე ათწილადად გადაქცევა ისეთი ჩვეულებრივი წილადი, რომლის მნიშვნელი არ შეიცავს 2-ისა და 5-ის გარდა სხვა გამყოფებს? მოდით გავარკვიოთ! რომელ წილადს ეწოდება ათწილადი და იწერება წილადის ზოლის გარეშე? პასუხი: წილადი 10 მნიშვნელით; 100; 1000 და ა.შ. და თითოეული ეს რიცხვი არის პროდუქტი თანაბარიორი და ხუთეულის რაოდენობა. ფაქტიურად: 10=2 ·5 ; 100=2 ·5 ·2 ·5 ; 1000=2 ·5 ·2 ·5 ·2 ·5 და ა.შ.

შესაბამისად, შეუქცევადი ჩვეულებრივი წილადის მნიშვნელი უნდა იყოს წარმოდგენილი, როგორც ნამრავლი „ორი“ და „ხუთი“, შემდეგ კი გავამრავლოთ 2-ზე და (ან) 5-ზე ისე, რომ „ორი“ და „ხუთი“ ტოლი გახდეს. მაშინ წილადის მნიშვნელი იქნება 10 ან 100 ან 1000 და ა.შ. იმისთვის, რომ წილადის მნიშვნელობა არ შეიცვალოს, წილადის მრიცხველს ვამრავლებთ იმავე რიცხვზე, რომელზეც გავამრავლეთ მნიშვნელი.

გამოთქვით შემდეგი საერთო წილადები ათწილადების სახით:

გამოსავალი. თითოეული ეს წილადი შეუქცევადია. მოდით, თითოეული წილადის მნიშვნელი გავამრავლოთ მარტივ ფაქტორებად.

20=2·2·5. დასკვნა: ერთი "A" აკლია.

8=2·2·2. დასკვნა: სამი "A" აკლია.

25=5·5. დასკვნა: ორი „ორი“ აკლია.

კომენტარი.პრაქტიკაში, ისინი ხშირად არ იყენებენ მნიშვნელის ფაქტორიზაციას, არამედ უბრალოდ სვამენ კითხვას: რამდენზე უნდა გამრავლდეს მნიშვნელი ისე, რომ შედეგი იყოს ერთი ნულებთან (10 ან 100 ან 1000 და ა.შ.). შემდეგ კი მრიცხველი მრავლდება იმავე რიცხვზე.

ასე რომ, იმ შემთხვევაში ა)(მაგალითი 2) 20 რიცხვიდან შეგიძლიათ მიიღოთ 100 5-ზე გამრავლებით, შესაბამისად, თქვენ უნდა გაამრავლოთ მრიცხველი და მნიშვნელი 5-ზე.

Როდესაც ბ)(მაგალითი 2) 8 რიცხვიდან არ მიიღება რიცხვი 100, მაგრამ რიცხვი 1000 მიიღება 125-ზე გამრავლებით. წილადის მრიცხველიც (3) და მნიშვნელიც (8) მრავლდება 125-ზე.

Როდესაც V)(მაგალითი 2) 25-დან მიიღებთ 100-ს, თუ გაამრავლებთ 4-ზე. ეს ნიშნავს, რომ მრიცხველი 8 უნდა გამრავლდეს 4-ზე.

უსასრულო ათობითი წილადი, რომელშიც ერთი ან მეტი ციფრი უცვლელად მეორდება იმავე თანმიმდევრობით, ეწოდება პერიოდულიროგორც ათობითი. განმეორებადი ციფრების სიმრავლეს ამ წილადის პერიოდი ეწოდება. მოკლედ, წილადის წერტილი იწერება ერთხელ, ფრჩხილებში ჩასმული.

Როდესაც ბ)(მაგალითი 1) არის მხოლოდ ერთი განმეორებადი ციფრი და უდრის 6-ს. ამიტომ, ჩვენი შედეგი 0.66... ​​ასე ჩაიწერება: 0,(6) . ისინი კითხულობენ: ნულოვანი წერტილი, ექვსი პერიოდი.

თუ ათწილადსა და პირველ წერტილს შორის არის ერთი ან მეტი განუმეორებელი ციფრი, მაშინ ასეთ პერიოდულ წილადს ეწოდება შერეული პერიოდული წილადი.

შეუქცევადი საერთო წილადი, რომლის მნიშვნელი არის სხვებთან ერთადმულტიპლიკატორი შეიცავს მულტიპლიკატორს 2 ან 5 , ხდება შერეულიპერიოდული ფრაქცია.

დაწერეთ რიცხვები ათწილადის სახით:

ნებისმიერი რაციონალური რიცხვი შეიძლება დაიწეროს როგორც უსასრულო პერიოდული ათობითი წილადი.

დაწერეთ რიცხვები უსასრულო პერიოდული წილადის სახით.

გახსოვთ, როგორ ვთქვი პირველივე გაკვეთილზე ათწილადების შესახებ, რომ არის რიცხვითი წილადები, რომლებიც არ შეიძლება წარმოდგენილი იყოს ათწილადების სახით (იხ. გაკვეთილი „ათწილადები“)? ჩვენ ასევე ვისწავლეთ წილადების მნიშვნელების ფაქტორები, რათა დავინახოთ, იყო თუ არა სხვა რიცხვები 2-ისა და 5-ის გარდა.

ასე რომ: მოვიტყუე. და დღეს ჩვენ ვისწავლით თუ როგორ გადავიტანოთ აბსოლუტურად ნებისმიერი რიცხვითი წილადი ათწილადად. ამავდროულად, ჩვენ გავეცნობით წილადების მთელ კლასს უსასრულო მნიშვნელოვანი ნაწილით.

პერიოდული ათობითი არის ნებისმიერი ათწილადი, რომელიც:

1. მნიშვნელოვანი ნაწილი შედგება უსასრულო რაოდენობის ციფრებისგან;
2. გარკვეული ინტერვალებით, მნიშვნელოვანი ნაწილის რიცხვები მეორდება.

განმეორებადი ციფრების სიმრავლეს, რომლებიც ქმნიან მნიშვნელოვან ნაწილს, ეწოდება წილადის პერიოდულ ნაწილს, ხოლო ამ სიმრავლის ციფრთა რაოდენობას - წილადის პერიოდი. მნიშვნელოვანი ნაწილის დარჩენილ სეგმენტს, რომელიც არ მეორდება, ეწოდება არაპერიოდული ნაწილი.

ვინაიდან მრავალი განმარტება არსებობს, ღირს ამ წილადებიდან რამდენიმე დეტალურად განხილვა:

ეს ფრაქცია ყველაზე ხშირად ჩნდება პრობლემებში. არაპერიოდული ნაწილი: 0; პერიოდული ნაწილი: 3; პერიოდის ხანგრძლივობა: 1.

არაპერიოდული ნაწილი: 0,58; პერიოდული ნაწილი: 3; პერიოდის ხანგრძლივობა: ისევ 1.

არაპერიოდული ნაწილი: 1; პერიოდული ნაწილი: 54; პერიოდის ხანგრძლივობა: 2.

არაპერიოდული ნაწილი: 0; პერიოდული ნაწილი: 641025; პერიოდის ხანგრძლივობა: 6. მოხერხებულობისთვის განმეორებადი ნაწილები ერთმანეთისგან გამოყოფილია სივრცეთი - ეს არ არის აუცილებელი ამ გადაწყვეტაში.

არაპერიოდული ნაწილი: 3066; პერიოდული ნაწილი: 6; პერიოდის ხანგრძლივობა: 1.

როგორც ხედავთ, პერიოდული წილადის განმარტება ემყარება კონცეფციას რიცხვის მნიშვნელოვანი ნაწილი. ამიტომ, თუ დაგავიწყდათ რა არის, გირჩევთ გაიმეოროთ - იხილეთ გაკვეთილი "".

პერიოდულ ათობითი წილადზე გადასვლა

განვიხილოთ a /b ფორმის ჩვეულებრივი წილადი. მოდით გავამრავლოთ მისი მნიშვნელი პირველ ფაქტორებად. არსებობს ორი ვარიანტი:

1. გაფართოება შეიცავს მხოლოდ 2 და 5 ფაქტორებს. ეს წილადები ადვილად გარდაიქმნება ათწილადებად - იხილეთ გაკვეთილი „ათწილადები“. ჩვენ არ გვაინტერესებს ასეთი ხალხი;
2. გაფართოებაში არის რაღაც სხვა, გარდა 2-ისა და 5-ისა. ამ შემთხვევაში, წილადი არ შეიძლება წარმოდგენილი იყოს ათწილადად, მაგრამ შეიძლება გადაკეთდეს პერიოდულ ათწილადად.

პერიოდული ათობითი წილადის დასადგენად, თქვენ უნდა იპოვოთ მისი პერიოდული და არაპერიოდული ნაწილები. Როგორ? გადააქციეთ წილადი არასწორ წილადად და შემდეგ გაყავით მრიცხველი მნიშვნელზე კუთხის გამოყენებით.

შემდეგი მოხდება:

1. ჯერ გაიყოფა მთელი ნაწილი , თუ ის არსებობს;
2. ათობითი წერტილის შემდეგ შეიძლება იყოს რამდენიმე რიცხვი;
3. ცოტა ხნის შემდეგ ნომრები დაიწყება გაიმეორეთ.

Სულ ეს არის! ათწილადის შემდეგ განმეორებადი რიცხვები აღინიშნება პერიოდული ნაწილით, ხოლო წინ - არაპერიოდული ნაწილით.

დავალება. გადაიყვანეთ ჩვეულებრივი წილადები პერიოდულ ათწილადებად:

ყველა წილადი მთელი რიცხვის გარეშე, ამიტომ ჩვენ უბრალოდ ვყოფთ მრიცხველს მნიშვნელზე "კუთხით":

როგორც ხედავთ, ნარჩენები მეორდება. წილადი ჩავწეროთ „სწორი“ სახით: 1,733 ... = 1,7(3).

შედეგი არის წილადი: 0,5833 ... = 0,58(3).

მიწერეთ ნორმალური ფორმა: 4,0909 ... = 4,(09).

ვიღებთ წილადს: 0.4141 ... = 0.(41).

პერიოდული ათობითი წილადიდან ჩვეულებრივ წილადზე გადასვლა

განვიხილოთ პერიოდული ათობითი წილადი X = abc (a 1 b 1 c 1). საჭიროა მისი კლასიკურ „ორსართულიან“ გადაქცევა. ამისათვის შეასრულეთ ოთხი მარტივი ნაბიჯი:

1. იპოვეთ წილადის პერიოდი, ე.ი. დათვალეთ რამდენი ციფრია პერიოდულ ნაწილში. ეს იყოს რიცხვი k;
2. იპოვეთ გამოთქმის მნიშვნელობა X · 10 კ. ეს უდრის ათობითი წერტილის გადატანას სრული პერიოდიმარჯვნივ - იხილეთ გაკვეთილი „ათწილადების გამრავლება და გაყოფა“;
3. ორიგინალური გამოხატულება უნდა გამოკლდეს მიღებულ რიცხვს. ამ შემთხვევაში პერიოდული ნაწილი "იწვა" და რჩება საერთო წილადი;
4. იპოვეთ X მიღებულ განტოლებაში. ჩვენ ყველა ათობითი წილადს ვცვლით ჩვეულებრივ წილადებად.

დავალება. ჩვეულებრივზე შემცირება არასწორი ფრაქციანომრები:

• 9,(6);
• 32,(39);
• 0,30(5);
• 0,(2475).

ჩვენ ვმუშაობთ პირველ წილადთან: X = 9, (6) = 9,666 ...

ფრჩხილები შეიცავს მხოლოდ ერთ ციფრს, ამიტომ წერტილი არის k = 1. შემდეგ, ამ წილადს ვამრავლებთ 10 k = 10 1 = 10-ზე. გვაქვს:

10X = 10 9.6666... ​​= 96.666...

გამოვაკლოთ თავდაპირველი წილადი და ამოხსენით განტოლება:

10X − X = 96,666 ... − 9,666 ... = 96 − 9 = 87;
9X = 87;
X = 87/9 = 29/3.

ახლა გადავხედოთ მეორე წილადს. ასე რომ X = 32, (39) = 32.393939...

პერიოდი k = 2, ასე რომ გავამრავლოთ ყველაფერი 10 k = 10 2 = 100:

100X = 100 · 32.393939 ... = 3239.3939 ...

კვლავ გამოვაკლოთ საწყისი წილადი და ამოხსნათ განტოლება:

100X − X = 3239,3939 ... − 32,3939 ... = 3239 − 32 = 3207;
99X = 3207;
X = 3207/99 = 1069/33.

გადავიდეთ მესამე წილადზე: X = 0.30(5) = 0.30555... დიაგრამა იგივეა, ამიტომ მხოლოდ გამოთვლებს მივცემ:

პერიოდი k = 1 ⇒ გავამრავლოთ ყველაფერი 10 k = 10 1 = 10;

10X = 10 0.30555... = 3.05555...
10X − X = 3,0555 ... − 0,305555 ... = 2,75 = 11/4;
9X = 11/4;
X = (11/4): 9 = 11/36.

ბოლოს ბოლო წილადი: X = 0,(2475) = 0,2475 2475... ისევ მოხერხებულობისთვის პერიოდული ნაწილები ერთმანეთისგან გამოყოფილია სივრცეებით. Ჩვენ გვაქვს:

k = 4 ⇒ 10 k = 10 4 = 10,000;
10,000X = 10,000 0.2475 2475 = 2475.2475 ...
10000X − X = 2475,2475 ... − 0,2475 2475 ... = 2475;
9999X = 2475;
X = 2475: 9999 = 25/101.

უსასრულო ათწილადები

ათობითი წერტილის შემდეგ ათწილადები შეიძლება შეიცავდეს ციფრების უსასრულო რაოდენობას.

უსასრულო ათწილადები- ეს არის ათობითი წილადები, რომლებიც შეიცავს უსასრულო რიცხვს.

უსასრულო ათობითი წილადის სრულად ჩაწერა თითქმის შეუძლებელია, ამიტომ მათი დაწერისას ისინი შემოიფარგლება მხოლოდ გარკვეული სასრული რაოდენობის ციფრებით ათობითი წერტილის შემდეგ, რის შემდეგაც ისინი აყენებენ ელიფსისს, რაც მიუთითებს ციფრების უსასრულოდ გაგრძელებულ თანმიმდევრობაზე.

მაგალითი 1

მაგალითად, $0.443340831\dots ; 3.1415935432\წერტილები; 135.126730405\წერტილები; 4.33333333333\წერტილები; 676.68349349\dots$.

მოდით შევხედოთ ბოლო ორ უსასრულო ათწილადს. წილადში $4.33333333333\dots$ ციფრი $3$ უსასრულოდ მეორდება, ხოლო წილადში $676.68349349\dots$ რიცხვების ჯგუფი $3$, $4$ და $9$ მეორდება მესამე ათობითი ადგილიდან. ასეთ უსასრულო ათობითი წილადებს პერიოდული ეწოდება.

პერიოდული ათწილადები

პერიოდული ათწილადები(ან პერიოდული წილადები) არის უსასრულო ათწილადი წილადები, რომელთა ჩაწერისას გარკვეული რიცხვი ან რიცხვების ჯგუფი, რომელსაც ეწოდება წილადის პერიოდი, გაუთავებლად მეორდება გარკვეული ათობითი ადგილიდან).

მაგალითი 2

მაგალითად, პერიოდული წილადის პერიოდი $4.33333333333\dots$ არის ციფრი $3$, ხოლო წილადის პერიოდი $676.68349349\dots$ არის რიცხვების ჯგუფი $349$.

უსასრულო პერიოდული ათობითი წილადების დაწერის სიმოკლესთვის, ჩვეულებრივად არის ჩაწერილი წერტილი ერთხელ, ფრჩხილებში ჩასმა. მაგალითად, პერიოდულ წილადზე $4.33333333333\dots$ იწერება $4,(3)$, ხოლო პერიოდულ წილადზე $676.68349349\dots$ იწერება $676.68(349)$.

უსასრულო პერიოდული ათობითი წილადები მიიღება ჩვეულებრივი წილადების, რომელთა მნიშვნელები შეიცავს $2$ და $5$-ის გარდა პირველ ფაქტორებს ათწილადად გადაქცევით.

ნებისმიერი სასრული ათობითი წილადი (და მთელი რიცხვი) შეიძლება ჩაიწეროს პერიოდული წილადის სახით, უსასრულო რაოდენობის $0$-იანი ციფრების დამატებით მარჯვნივ.

მაგალითი 3

მაგალითად, სასრული ათობითი $45.12$ შეიძლება დაიწეროს პერიოდული წილადის სახით, როგორც $45.12(0)$, ხოლო მთელი რიცხვი $(74)$, როგორც უსასრულო პერიოდული ათწილადი იქნება $74(0)$.

პერიოდული წილადების შემთხვევაში, რომლებსაც აქვთ პერიოდი 9, გამოიყენეთ გადასვლა პერიოდული წილადის სხვა აღნიშვნაზე $0$ პერიოდით. მხოლოდ ამ მიზნით მე-9 პერიოდი იცვლება $0$ პერიოდით, ხოლო შემდეგი უმაღლესი ციფრის ღირებულება იზრდება $1$-ით.

მაგალითი 4

მაგალითად, პერიოდული წილადი $7.45(9)$ შეიძლება შეიცვალოს პერიოდული წილადით $7.46(0)$ ან ექვივალენტური ათობითი წილადი $7.46$.

უსასრულო ათობითი პერიოდული წილადები წარმოდგენილია რაციონალური რიცხვებით. სხვა სიტყვებით რომ ვთქვათ, ნებისმიერი პერიოდული წილადი შეიძლება გარდაიქმნას საერთო წილადად და ნებისმიერი საერთო წილადი შეიძლება იყოს წარმოდგენილი როგორც პერიოდული წილადი.

წილადების გადაყვანა სასრულ და უსასრულო პერიოდულ ათწილადებად

არა მხოლოდ ჩვეულებრივი წილადები $10, 100, \dots$ მნიშვნელებით შეიძლება გადაიზარდოს ათობითი წილადად.

ზოგიერთ შემთხვევაში, თავდაპირველი საერთო წილადი ადვილად შეიძლება შემცირდეს $10$, $100$ ან $1\000$ მნიშვნელამდე, რის შემდეგაც მიღებული წილადი შეიძლება იყოს წარმოდგენილი ათწილადის სახით.

მაგალითი 5

$\frac(3)(5)$ წილადის გადასაყვანად წილადად $10$ მნიშვნელით, თქვენ უნდა გაამრავლოთ წილადის მრიცხველი და მნიშვნელი $2$-ზე, რის შემდეგაც მივიღებთ $\frac(6)( 10)$, რომლის თარგმნა არც ისე რთულია ათწილადის წილადზე $0.6$.

სხვა შემთხვევებისთვის გამოიყენება საერთო წილადის ათწილადად გადაქცევის სხვა მეთოდი):

მრიცხველი უნდა შეიცვალოს ათწილადი წილადით ნებისმიერი რაოდენობის ნულებით ათობითი წერტილის შემდეგ;

წილადის მრიცხველი გავყოთ მნიშვნელზე (გაყოფა შესრულებულია ნატურალური რიცხვების სვეტად დაყოფის სახით, ხოლო კოეფიციენტში ათწილადი მოთავსებულია დივიდენდის მთელი ნაწილის გაყოფის დასრულების შემდეგ).

მაგალითი 6

გადააქციეთ წილადი $\frac(621)(4)$ ათწილადად.

გამოსავალი.

წარმოვიდგინოთ რიცხვი $621$ მრიცხველში ათწილადის სახით. ამისათვის დაამატეთ ათობითი წერტილი და, დასაწყისისთვის, ორი ნული მის შემდეგ. შემდეგ, საჭიროების შემთხვევაში, შეგიძლიათ დაამატოთ მეტი ნული. ასე რომ, ჩვენ მივიღეთ $621.00$.

მოდით გავყოთ რიცხვი $621.00$ $4$-ზე სვეტად:

სურათი 1.

გაყოფამ მიაღწია დივიდენდში ათწილადს და ნაშთი არ იყო ნული. ამ შემთხვევაში, ათწილადი მოთავსებულია კოეფიციენტში და დაყოფა გრძელდება სვეტში, მძიმეების მიუხედავად:

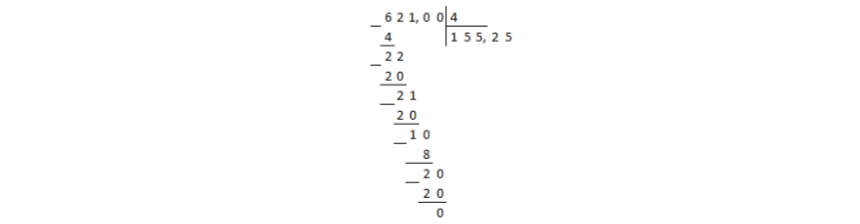
სურათი 2.

ნაშთი არის ნული, რაც ნიშნავს, რომ გაყოფა დასრულდა.

უპასუხე: $155,25$.

შესაძლებელია, რომ ჩვეულებრივი წილადის მრიცხველისა და მნიშვნელის გაყოფისას, ნაშთი არ გამოვიდეს $0$. ამ შემთხვევაში, გაყოფა შეიძლება გაგრძელდეს განუსაზღვრელი ვადით. გარკვეული მომენტიდან დაწყებული გაყოფის ნაშთები პერიოდულად მეორდება, რაც იმას ნიშნავს, რომ კოეფიციენტში მოცემული რიცხვებიც მეორდება. აქედან შეგვიძლია დავასკვნათ, რომ ეს ჩვეულებრივი წილადი გარდაიქმნება უსასრულო პერიოდულ ათობითი წილადად.

მაგალითი 7

გადააქციეთ წილადი $\frac(19)(44)$ ათწილადად.

გამოსავალი.)

საერთო წილადის ათწილადად გადასაყვანად, შეასრულეთ გრძელი გაყოფა:

სურათი 3.

გაყოფისას მეორდება ნაშთები $8$ და $36$ და კოეფიციენტში ასევე მეორდება რიცხვები $1$ და $8$. ასე რომ, საწყისი ჩვეულებრივი წილადი $\frac(19)(44)$ გადაკეთდა პერიოდულ წილადად $\frac(19)(44)=0.43181818\dots =0.43(18)$.

პასუხი: $0,43(18)$.

ზოგადი დასკვნა ჩვეულებრივი წილადების ათწილადებად გადაქცევის შესახებ:

თუ მნიშვნელი შეიძლება დაიშალოს მარტივ ფაქტორებად, რომელთა შორის იქნება მხოლოდ რიცხვები $2$ და $5$, მაშინ ასეთი წილადი შეიძლება გარდაიქმნას საბოლოო ათობითი წილადად;

თუ $2$ და $5$ რიცხვების გარდა, მნიშვნელის გაფართოება შეიცავს სხვა მარტივ რიცხვებს, მაშინ ასეთი წილადი გარდაიქმნება უსასრულო ათობითი პერიოდულ წილადად.