Denne artikkelen handler om desimaler. Her skal vi forstå desimalnotasjonen av brøktall, introdusere begrepet en desimalbrøk og gi eksempler på desimalbrøker. Deretter skal vi snakke om sifrene til desimalbrøker og gi navnene på sifrene. Etter dette vil vi fokusere på uendelige desimalbrøker, la oss snakke om periodiske og ikke-periodiske brøker. Nedenfor lister vi opp hovedhandlingene med desimaler. Avslutningsvis, la oss bestemme plasseringen av desimalbrøkene på koordinatbjelken.
Sidenavigering.
Desimalnotasjon av et brøktall
Leser desimaler
La oss si noen ord om reglene for lesing av desimalbrøker.
Desimalbrøker, som tilsvarer egentlige ordinære brøker, leses på samme måte som disse ordinære brøkene, kun "null heltall" legges først til. For eksempel tilsvarer desimalbrøken 0,12 den vanlige brøken 12/100 (les "tolv hundredeler"), derfor leses 0,12 som "null komma tolv hundredeler".
Desimalbrøker som tilsvarer blandede tall leses nøyaktig likt som disse blandede tallene. For eksempel tilsvarer desimalbrøken 56.002 et blandet tall, så desimalbrøken 56.002 leses som "femtiseks komma to tusendeler."
Plasser i desimaler
Skrive desimalbrøker, så vel som skriftlig naturlige tall, betydningen av hvert siffer avhenger av dets posisjon. Faktisk betyr tallet 3 i desimalbrøken 0,3 tre tideler, i desimalbrøken 0,0003 - tre ti tusendeler, og i desimalbrøken 30 000,152 - tre titusener. Så vi kan snakke om desimaler, samt om sifrene i naturlige tall.
Navnene på sifrene i desimalbrøken opp til desimaltegnet er fullstendig sammenfallende med navnene på sifrene i naturlige tall. Og navnene på desimalplassene etter desimaltegnet kan sees fra følgende tabell.

For eksempel, i desimalbrøken 37.051 er sifferet 3 på tierplassen, 7 er på enhetsplassen, 0 er på tiendedelsplassen, 5 er på hundredelersplassen og 1 er på tusendelsplassen.
Plasser i desimalbrøker er også forskjellige i forrang. Hvis vi ved å skrive en desimalbrøk flytter fra siffer til siffer fra venstre til høyre, så flytter vi fra seniorer Til junior rekker. For eksempel er hundredelsplassen eldre enn tiendedelsplassen, og millionplassen er lavere enn hundredelsplassen. I en gitt siste desimalbrøk kan vi snakke om de store og små sifrene. For eksempel i desimalbrøk 604,9387 senior (høyest) stedet er hundreplassen, og junior (laveste)- ti tusendels siffer.
For desimalbrøker skjer ekspansjon til sifre. Det ligner på ekspansjon til sifre med naturlige tall. For eksempel er utvidelsen til desimaler på 45,6072 som følger: 45,6072=40+5+0,6+0,007+0,0002. Og egenskapene til addisjon fra dekomponeringen av en desimalbrøk til sifre lar deg gå videre til andre representasjoner av denne desimalbrøken, for eksempel 45,6072=45+0,6072, eller 45,6072=40,6+5,007+0,0002, eller 45,45700=7,45720. 0,6.
Sluttdesimaler
Frem til dette punktet har vi bare snakket om desimalbrøker, i notasjonen som det er et endelig antall sifre etter desimaltegnet. Slike brøker kalles endelige desimaler.
Definisjon.
Sluttdesimaler- Dette er desimalbrøker, hvor postene inneholder et begrenset antall tegn (siffer).
Her er noen eksempler på endelige desimalbrøker: 0,317, 3,5, 51,1020304958, 230 032,45.
Imidlertid kan ikke hver brøk representeres som en siste desimal. For eksempel kan ikke brøken 5/13 erstattes med en lik brøk med en av nevnerne 10, 100, ..., og kan derfor ikke konverteres til en endelig desimalbrøk. Vi vil snakke mer om dette i teoridelen, å konvertere vanlige brøker til desimaler.
Uendelige desimaler: Periodiske brøker og ikke-periodiske brøker
Når du skriver en desimalbrøk etter desimaltegnet, kan du anta muligheten for et uendelig antall sifre. I dette tilfellet vil vi komme til å vurdere de såkalte uendelige desimalbrøkene.
Definisjon.
Uendelige desimaler– Dette er desimalbrøker, som inneholder et uendelig antall sifre.
Det er klart at vi ikke kan skrive ned uendelige desimalbrøker i full form, så i deres registrering begrenser vi oss til bare et visst begrenset antall sifre etter desimaltegnet og setter en ellipse som indikerer en uendelig kontinuerlig sekvens av sifre. Her er noen eksempler på uendelige desimalbrøker: 0,143940932…, 3,1415935432…, 153,02003004005…, 2,111111111…, 69,74152152152….
Hvis du ser nøye på de to siste uendelige desimalbrøkene, så i brøken 2.111111111... er det endeløst gjentakende tallet 1 godt synlig, og i brøken 69.74152152152..., med utgangspunkt i tredje desimal, en gjentatt gruppe tall 1, 5 og 2 er godt synlige. Slike uendelige desimalbrøker kalles periodiske.
Definisjon.
Periodiske desimaler(eller rett og slett periodiske brøker) er endeløse desimalbrøker, i registreringen av hvilke, fra en viss desimal, gjentas et eller annet tall eller gruppe av tall uendelig, som kalles periode av brøken.
For eksempel er perioden for den periodiske brøken 2.111111111... sifferet 1, og perioden for brøken 69.74152152152... er en gruppe sifre med formen 152.
For uendelige periodiske desimalbrøker er det akseptert spesiell form poster. For korthets skyld ble vi enige om å skrive ned perioden én gang, og sette den i parentes. For eksempel skrives den periodiske brøken 2.111111111... som 2,(1) , og den periodiske brøken 69.74152152152... skrives som 69.74(152) .
Det er verdt å merke seg at for den samme periodiske desimalbrøken kan du spesifisere ulike perioder. For eksempel kan den periodiske desimalbrøken 0,73333... betraktes som en brøk 0,7(3) med en periode på 3, og også som en brøk 0,7(33) med en periode på 33, og så videre 0,7(333), 0,7 (3333), ... Du kan også se på den periodiske brøken 0,73333 ... slik: 0,733(3), eller slik 0,73(333), osv. Her, for å unngå tvetydighet og uoverensstemmelser, er vi enige om å betrakte som perioden av en desimalbrøk den korteste av alle mulige sekvenser av repeterende sifre, og starte fra nærmeste posisjon til desimaltegnet. Det vil si at perioden for desimalbrøken 0,73333... vil bli betraktet som en sekvens av ett siffer 3, og periodisiteten starter fra den andre posisjonen etter desimalpunktet, det vil si 0,73333...=0,7(3). Et annet eksempel: den periodiske brøken 4,7412121212... har en periode på 12, periodisiteten starter fra det tredje sifferet etter desimaltegnet, det vil si 4,7412121212...=4,74(12).
Uendelige periodiske desimalbrøker oppnås når de konverteres til desimalbrøker vanlige brøker, hvis nevnere inneholder andre primfaktorer enn 2 og 5.
Her er det verdt å nevne periodiske brøker med en periode på 9. La oss gi eksempler på slike brøker: 6.43(9) , 27,(9) . Disse brøkene er en annen notasjon for periodiske brøker med periode 0, og de erstattes vanligvis med periodiske brøker med periode 0. For å gjøre dette erstattes periode 9 med periode 0, og verdien av det nest høyeste sifferet økes med én. For eksempel erstattes en brøk med periode 9 på formen 7.24(9) med en periodebrøk med periode 0 på formen 7.25(0) eller en lik siste desimalbrøk 7.25. Et annet eksempel: 4,(9)=5,(0)=5. Likheten til en brøk med periode 9 og dens tilsvarende brøk med periode 0 er lett å etablere etter å ha erstattet disse desimalbrøkene med like vanlige brøker.
Til slutt, la oss se nærmere på uendelige desimalbrøker, som ikke inneholder en uendelig repeterende sekvens av sifre. De kalles ikke-periodiske.
Definisjon.
Engangsdesimaler(eller rett og slett ikke-periodiske brøker) er uendelige desimalbrøker som ikke har noen punktum.
Noen ganger har ikke-periodiske brøker en form som ligner på periodiske brøker, for eksempel er 8.02002000200002... en ikke-periodisk brøk. I disse tilfellene bør du være spesielt forsiktig med å merke forskjellen.
Merk at ikke-periodiske brøker ikke konverteres til vanlige brøker; uendelige ikke-periodiske desimalbrøker representerer irrasjonelle tall.
Operasjoner med desimaler
En av operasjonene med desimalbrøker er sammenligning, og de fire grunnleggende aritmetiske funksjonene er også definert operasjoner med desimaler: addisjon, subtraksjon, multiplikasjon og divisjon. La oss vurdere separat hver av handlingene med desimalbrøker.
Sammenligning av desimaler i hovedsak basert på sammenligning av vanlige brøker som tilsvarer desimalbrøkene som sammenlignes. Å konvertere desimalbrøker til vanlige brøker er imidlertid en ganske arbeidskrevende prosess, og uendelige ikke-periodiske brøker kan ikke representeres som en ordinær brøk, så det er praktisk å bruke en stedsmessig sammenligning av desimalbrøker. Stedsvis sammenligning av desimalbrøker ligner på sammenligning av naturlige tall. For mer detaljert informasjon anbefaler vi å studere artikkelen: sammenligning av desimalbrøker, regler, eksempler, løsninger.
La oss gå videre til neste handling - multiplisere desimaler. Multiplikasjon av endelige desimalbrøker utføres på samme måte som subtraksjon av desimalbrøker, regler, eksempler, løsninger på multiplikasjon med en kolonne med naturlige tall. Ved periodiske brøker kan multiplikasjon reduseres til multiplikasjon av vanlige brøker. I sin tur reduseres multiplikasjonen av uendelige ikke-periodiske desimalbrøker etter deres avrunding til multiplikasjonen av endelige desimalbrøker. Vi anbefaler for videre studier av materialet i artikkelen: multiplikasjon av desimalbrøker, regler, eksempler, løsninger.
Desimaler på en koordinatstråle
Det er en en-til-en samsvar mellom poeng og desimaler.
La oss finne ut hvordan punkter på koordinatstrålen er konstruert som tilsvarer en gitt desimalbrøk.
Vi kan erstatte endelige desimalbrøker og uendelige periodiske desimalbrøker med like vanlige brøker, og så konstruere de tilsvarende ordinære brøkene på koordinatstrålen. For eksempel tilsvarer desimalbrøken 1.4 fellesbrøken 14/10, så punktet med koordinat 1.4 fjernes fra origo i positiv retning med 14 segmenter lik en tiendedel av et enhetssegment.

Desimalbrøker kan merkes på en koordinatstråle, med utgangspunkt i dekomponeringen av en gitt desimalbrøk til sifre. La oss for eksempel bygge et punkt med koordinat 16.3007, siden 16.3007=16+0.3+0.0007, så kan vi komme til dette punktet ved å sekvensielt legge 16 enhetssegmenter fra opprinnelsen til koordinatene, 3 segmenter hvis lengde er lik en tiendedel av en enhet, og 7 segmenter, hvis lengde er lik en titusendel av et enhetssegment.
Denne måten å bygge på desimaltall på koordinatstrålen lar deg komme så nært du vil punktet som tilsvarer den uendelige desimalbrøken.
Noen ganger er det mulig å plotte nøyaktig punktet som tilsvarer en uendelig desimalbrøk. For eksempel, ![]() , så tilsvarer denne uendelige desimalbrøken 1,41421... et punkt på koordinatstrålen, fjernt fra origo på koordinatene med lengden på diagonalen til et kvadrat med en side av 1 enhetssegment.
, så tilsvarer denne uendelige desimalbrøken 1,41421... et punkt på koordinatstrålen, fjernt fra origo på koordinatene med lengden på diagonalen til et kvadrat med en side av 1 enhetssegment.
Den omvendte prosessen med å få desimalbrøken som tilsvarer et gitt punkt på en koordinatstråle er den s.k. desimalmåling av et segment. La oss finne ut hvordan det gjøres.
La vår oppgave være å komme fra origo til et gitt punkt på koordinatlinjen (eller å nærme seg det uendelig hvis vi ikke kan komme til det). Med desimalmåling av et segment, kan vi sekvensielt fjerne et hvilket som helst antall enhetssegmenter fra origo, deretter segmenter hvis lengde er lik en tiendedel av en enhet, deretter segmenter hvis lengde er lik en hundredel av en enhet, osv. Ved å registrere antall segmenter av hver lengde som legges til side, får vi desimalbrøken som tilsvarer et gitt punkt på koordinatstrålen.
For å komme til punkt M i figuren ovenfor, må du for eksempel sette til side 1 enhetssegment og 4 segmenter, hvis lengde er lik en tiendedel av en enhet. Dermed tilsvarer punkt M desimalbrøken 1,4.
Det er klart at punktene til koordinatstrålen, som ikke kan nås i prosessen med desimalmåling, tilsvarer uendelige desimalbrøker.
Bibliografi.
- Matematikk: lærebok for 5. klasse. allmennutdanning institusjoner / N. Ya. Vilenkin, V. I. Zhokhov, A. S. Chesnokov, S. I. Shvartsburd. - 21. utg., slettet. - M.: Mnemosyne, 2007. - 280 s.: ill. ISBN 5-346-00699-0.
- Matematikk. 6. klasse: lærerikt. for allmennutdanning institusjoner / [N. Ya. Vilenkin og andre]. - 22. utgave, rev. - M.: Mnemosyne, 2008. - 288 s.: ill. ISBN 978-5-346-00897-2.
- Algebra: lærebok for 8. klasse. allmennutdanning institusjoner / [Yu. N. Makarychev, N.G. Mindyuk, K.I. Neshkov, S.B. Suvorova]; redigert av S. A. Telyakovsky. - 16. utg. - M.: Utdanning, 2008. - 271 s. : jeg vil. - ISBN 978-5-09-019243-9.
- Gusev V.A., Mordkovich A.G. Matematikk (en manual for de som går inn på tekniske skoler): Proc. godtgjørelse.- M.; Høyere skole, 1984.-351 s., ill.
Som kjent inkluderer settet med rasjonelle tall (Q) settet med heltall (Z), som igjen inkluderer settet med naturlige tall (N). I tillegg til hele tall inkluderer rasjonelle tall brøker.
Hvorfor blir da hele settet med rasjonelle tall noen ganger betraktet som uendelige periodiske desimalbrøker? Faktisk, i tillegg til brøker, inkluderer de også heltall, så vel som ikke-periodiske brøker.
Faktum er at alle heltall, så vel som enhver brøk, kan representeres som en uendelig periodisk desimalbrøk. Det vil si at for alle rasjonelle tall kan du bruke samme registreringsmetode.
Hvordan er en uendelig periodisk desimal representert? I den er en gjentatt gruppe med tall etter desimaltegnet plassert i parentes. For eksempel er 1,56(12) en brøk der siffergruppen 12 gjentas, det vil si at brøken har verdien 1,561212121212... og så videre i det uendelige. En gjentatt gruppe med tall kalles en periode.
Imidlertid kan vi representere et hvilket som helst tall i denne formen hvis vi anser perioden for å være tallet 0, som også gjentas i det uendelige. For eksempel er tallet 2 det samme som 2,00000.... Derfor kan det skrives som en uendelig periodisk brøk, dvs. 2,(0).
Det samme kan gjøres med hvilken som helst endelig brøk. For eksempel:
0,125 = 0,1250000... = 0,125(0)
Imidlertid bruker de i praksis ikke transformasjonen av en endelig brøk til en uendelig periodisk. Derfor skiller de endelige brøker og uendelige periodiske. Dermed er det mer riktig å si at de rasjonelle tallene inkluderer
- alle heltall
- siste fraksjoner,
- uendelige periodiske brøker.
Samtidig må du bare huske at heltall og endelige brøker er representable i teorien i form av uendelige periodiske brøker.
På den annen side er begrepene endelig og uendelig brøkdel gjelder for desimalbrøker. Når det gjelder brøker, kan både endelige og uendelige desimaler representeres unikt som en brøk. Dette betyr at fra vanlige brøkers synspunkt er periodiske og endelige brøker det samme. I tillegg kan hele tall også representeres som en brøk ved å forestille oss at vi deler tallet med 1.
Hvordan representere en desimal uendelig periodisk brøk som en vanlig brøk? Den mest brukte algoritmen er noe sånt som dette:
- Reduser brøken slik at det bare er en punktum etter desimaltegnet.
- Multipliser en uendelig periodisk brøk med 10 eller 100 eller ... slik at desimaltegnet flyttes til høyre med én punktum (dvs. en periode ender opp i hele delen).
- Lik den opprinnelige brøken (a) med variabelen x, og brøken (b) oppnådd ved å multiplisere med tallet N til Nx.
- Trekk fra x fra Nx. Fra b trekker jeg a. Det vil si at de utgjør ligningen Nx – x = b – a.
- Når man løser en ligning, er resultatet en vanlig brøk.
Et eksempel på å konvertere en uendelig periodisk desimalbrøk til en vanlig brøk:
x = 1,13333...
10x = 11,3333...
10x * 10 = 11,33333... * 10
100x = 113,3333...
100x – 10x = 113,3333... – 11,3333...
90x = 102
x =
For å skrive et rasjonelt tall m/n som en desimalbrøk, må du dele telleren på nevneren. I dette tilfellet skrives kvotienten som en endelig eller uendelig desimalbrøk.
Skrive ned gitt nummer som en desimalbrøk.
Løsning. Del telleren for hver brøk i en kolonne med nevneren: EN) del 6 med 25; b) del 2 med 3; V) del 1 med 2, og legg deretter den resulterende brøken til en - heltallsdelen av dette blandede tallet.

Irreduserbare vanlige brøker hvis nevnere ikke inneholder andre primfaktorer enn 2 Og 5 , skrives som en siste desimalbrøk.
I eksempel 1 når EN) nevner 25=5·5; når V) nevneren er 2, så vi får de siste desimalene 0,24 og 1,5. Når b) nevneren er 3, så resultatet kan ikke skrives som en endelig desimal.
Er det mulig, uten lang divisjon, å gjøre om til en desimalbrøk en slik vanlig brøk, hvis nevner ikke inneholder andre divisorer enn 2 og 5? La oss finne ut av det! Hvilken brøk kalles en desimal og skrives uten brøkstrek? Svar: brøk med nevner 10; 100; 1000 osv. Og hvert av disse tallene er et produkt lik antall toere og femmere. Faktisk: 10=2 ·5; 100=2 ·5 ·2 ·5; 1000=2 ·5 ·2 ·5 ·2 ·5 osv.
Følgelig må nevneren til en irreduserbar ordinær brøk representeres som produktet av "toer" og "fem", og deretter multiplisert med 2 og (eller) 5 slik at "toere" og "femere" blir like. Da vil nevneren til brøken være lik 10 eller 100 eller 1000 osv. For å sikre at verdien av brøken ikke endres, multipliserer vi telleren til brøken med det samme tallet som vi multipliserte nevneren med.
Uttrykk følgende vanlige brøker som desimaler:
![]()
Løsning. Hver av disse fraksjonene er irreduserbare. La oss faktorisere nevneren til hver brøk i primfaktorer.
20=2·2·5. Konklusjon: en "A" mangler.
8=2·2·2. Konklusjon: tre "A" mangler.
25=5·5. Konklusjon: to "toere" mangler.

Kommentar. I praksis bruker de ofte ikke faktorisering av nevneren, men stiller rett og slett spørsmålet: hvor mye skal nevneren multipliseres slik at resultatet blir én med nuller (10 eller 100 eller 1000 osv.). Og så multipliseres telleren med det samme tallet.
Så i tilfelle EN)(eksempel 2) fra tallet 20 kan du få 100 ved å multiplisere med 5, derfor må du gange telleren og nevneren med 5.
Når b)(eksempel 2) fra tallet 8 vil ikke tallet 100 fås, men tallet 1000 oppnås ved å multiplisere med 125. Både telleren (3) og nevneren (8) til brøken multipliseres med 125.
Når V)(eksempel 2) fra 25 får du 100 hvis du multipliserer med 4. Dette betyr at telleren 8 må ganges med 4.
En uendelig desimalbrøk der ett eller flere sifre alltid gjentas i samme rekkefølge kalles periodisk som en desimal. Settet med repeterende sifre kalles perioden for denne brøkdelen. For korthets skyld skrives perioden til en brøk én gang, omsluttet i parentes.
Når b)(eksempel 1) det er bare ett repeterende siffer og er lik 6. Derfor vil resultatet vårt 0,66... skrives slik: 0,(6) . De leste: null poeng, seks i punktum.
Hvis det er ett eller flere ikke-repeterende sifre mellom desimaltegn og første punktum, kalles en slik periodisk brøk en blandet periodisk brøk.
En irreduserbar fellesbrøk hvis nevner er sammen med andre multiplikator inneholder multiplikator 2 eller 5 , blir blandet periodisk brøk.
Skriv tallene som en desimalbrøk:
![]()
Ethvert rasjonelt tall kan skrives som en uendelig periodisk desimalbrøk.
Skriv tallene som en uendelig periodisk brøk.
Husker du hvordan jeg i den aller første leksjonen om desimaler sa at det er numeriske brøker som ikke kan representeres som desimaler (se leksjonen "Desimaler")? Vi lærte også å faktorisere nevnerne til brøker for å se om det fantes andre tall enn 2 og 5.
Så: Jeg løy. Og i dag vil vi lære hvordan du konverterer absolutt enhver numerisk brøk til en desimal. Samtidig vil vi bli kjent med en hel klasse brøker med en uendelig betydelig del.
En periodisk desimal er enhver desimal som:
- Den signifikante delen består av et uendelig antall sifre;
- Ved visse intervaller gjentas tallene i den betydelige delen.
Settet med repeterende sifre som utgjør den signifikante delen kalles den periodiske delen av en brøk, og antall sifre i dette settet kalles perioden for brøken. Det gjenværende segmentet av den betydelige delen, som ikke gjentas, kalles den ikke-periodiske delen.
Siden det er mange definisjoner, er det verdt å vurdere noen av disse brøkene i detalj:
Denne brøken vises oftest i problemer. Ikke-periodisk del: 0; periodisk del: 3; periodelengde: 1.
Ikke-periodisk del: 0,58; periodisk del: 3; periodelengde: igjen 1.
Ikke-periodisk del: 1; periodisk del: 54; periodelengde: 2.
Ikke-periodisk del: 0; periodisk del: 641025; periodelengde: 6. For enkelhets skyld er repeterende deler atskilt fra hverandre med et mellomrom - dette er ikke nødvendig i denne løsningen.
Ikke-periodisk del: 3066; periodisk del: 6; periodelengde: 1.
Som du kan se, er definisjonen av en periodisk brøk basert på konseptet betydelig del av et tall. Derfor, hvis du har glemt hva det er, anbefaler jeg å gjenta det - se leksjonen "".
Overgang til periodisk desimalbrøk
Betrakt en vanlig brøkdel av formen a /b. La oss faktorisere nevneren til primfaktorer. Det er to alternativer:
- Utvidelsen inneholder kun faktor 2 og 5. Disse brøkene konverteres enkelt til desimaler - se leksjonen "Desimaler". Vi er ikke interessert i slike mennesker;
- Det er noe annet i utvidelsen enn 2 og 5. I dette tilfellet kan ikke brøken representeres som en desimal, men den kan konverteres til en periodisk desimal.
For å definere en periodisk desimalbrøk, må du finne dens periodiske og ikke-periodiske deler. Hvordan? Konverter brøken til en uekte brøk, og del deretter telleren med nevneren ved å bruke et hjørne.
Følgende vil skje:
- Skal splittes først hele delen , hvis det finnes;
- Det kan være flere tall etter desimaltegn;
- Etter en stund begynner tallene gjenta.
Det er alt! Gjentatte tall etter desimaltegnet er merket med den periodiske delen, og de foran er merket med den ikke-periodiske delen.
Oppgave. Konverter vanlige brøker til periodiske desimaler:
Alle brøker uten en heltallsdel, så vi deler ganske enkelt telleren med nevneren med et "hjørne":

Som du kan se, gjentas resten. La oss skrive brøken i "riktig" form: 1,733 ... = 1,7(3).

Resultatet er en brøk: 0,5833 ... = 0,58(3).

Skrive til normal form: 4,0909 ... = 4,(09).

Vi får brøken: 0,4141 ... = 0,(41).
Overgang fra periodisk desimalbrøk til vanlig brøk
Tenk på den periodiske desimalbrøken X = abc (a 1 b 1 c 1). Det er nødvendig å konvertere den til en klassisk "to-etasjers". For å gjøre dette, følg fire enkle trinn:
- Finn perioden til brøken, dvs. tell hvor mange sifre som er i den periodiske delen. La dette være tallet k;
- Finn verdien av uttrykket X · 10 k. Dette tilsvarer å flytte desimaltegnet med full periode til høyre - se leksjonen "Multipisere og dele desimaler";
- Det opprinnelige uttrykket må trekkes fra det resulterende tallet. I dette tilfellet blir den periodiske delen "brent" og forblir vanlig brøk;
- Finn X i den resulterende ligningen. Vi konverterer alle desimalbrøker til vanlige brøker.
Oppgave. Reduser til vanlig uekte brøk tall:
- 9,(6);
- 32,(39);
- 0,30(5);
- 0,(2475).
Vi jobber med den første brøken: X = 9,(6) = 9,666 ...
Parentesen inneholder kun ett siffer, så perioden er k = 1. Deretter multipliserer vi denne brøken med 10 k = 10 1 = 10. Vi har:
10X = 10 9,6666... = 96,666...
Trekk fra den opprinnelige brøken og løs likningen:
10X − X = 96,666 ... − 9,666 ... = 96 − 9 = 87;
9X = 87;
X = 87/9 = 29/3.
La oss nå se på den andre brøken. Så X = 32,(39) = 32,393939...
Periode k = 2, så multipliser alt med 10 k = 10 2 = 100:
100X = 100 · 32,393939 ... = 3239,3939 ...
Trekk fra den opprinnelige brøken igjen og løs likningen:
100X − X = 3239,3939 ... − 32,3939 ... = 3239 − 32 = 3207;
99X = 3207;
X = 3207/99 = 1069/33.
La oss gå videre til den tredje brøken: X = 0,30(5) = 0,30555... Diagrammet er det samme, så jeg vil bare gi beregningene:
Periode k = 1 ⇒ multipliser alt med 10 k = 10 1 = 10;
10X = 10 0,30555... = 3,05555...
10X − X = 3,0555 ... − 0,305555 ... = 2,75 = 11/4;
9X = 11/4;
X = (11/4): 9 = 11/36.
Til slutt, den siste brøken: X = 0,(2475) = 0,2475 2475... Igjen, for enkelhets skyld er de periodiske delene atskilt fra hverandre med mellomrom. Vi har:
k = 4 ⇒ 10 k = 10 4 = 10 000;
10 000X = 10 000 0,2475 2475 = 2475,2475 ...
10 000X − X = 2475,2475 ... − 0,2475 2475 ... = 2475;
9999X = 2475;
X = 2475: 9999 = 25/101.
Uendelige desimaler
Desimaler etter desimaltegn kan inneholde et uendelig antall sifre.
Uendelige desimaler- dette er desimalbrøker, som inneholder et uendelig antall sifre.
En uendelig desimalbrøk er nesten umulig å skrive ned fullstendig, så når du skriver dem, er de begrenset til bare et visst begrenset antall sifre etter desimaltegn, hvoretter de setter en ellipse, som indikerer en uendelig kontinuerlig sekvens av sifre.
Eksempel 1
For eksempel, $0,443340831\dots ; 3.1415935432\prikker ; 135.126730405\prikker ; 4.33333333333\prikker ; 676.68349349\dots$.
La oss se på de to siste uendelige desimalene. I brøken $4.33333333333\dots$ gjentas sifferet $3$ i det uendelige, og i brøken $676.68349349\dots$ gjentas sifregruppen $3$, $4$ og $9$ fra tredje desimal. Slike uendelige desimalbrøker kalles periodiske.
Periodiske desimaler
Periodiske desimaler(eller periodiske brøker) er uendelige desimalbrøker, i registreringen av hvilke et eller annet tall eller gruppe med tall, kalt perioden for brøken, gjentas i det uendelige fra et bestemt desimalsted).
Eksempel 2
For eksempel er perioden for den periodiske brøken $4,33333333333\dots$ sifferet $3$, og perioden for brøken $676,68349349\dots$ er gruppen av sifre $349$.
For korthets skyld ved å skrive uendelige periodiske desimalbrøker, er det vanlig å skrive punktum én gang, og omslutte den i parentes. For eksempel skrives den periodiske brøken $4,333333333333\dots$ $4,(3)$, og den periodiske brøken $676,68349349\dots$ skrives $676,68(349)$.
Uendelige periodiske desimalbrøker oppnås ved å konvertere vanlige brøker hvis nevnere inneholder andre primfaktorer enn $2$ og $5$ til desimalbrøker.
Enhver endelig desimalbrøk (og heltall) kan skrives som en periodisk brøk ved å legge til et uendelig antall sifre $0$ til høyre.
Eksempel 3
For eksempel kan den endelige desimalen $45,12$ skrives som en periodisk brøk som $45,12(0)$, og heltallet $(74)$ som en uendelig periodisk desimal vil være $74(0)$.
Når det gjelder periodiske brøker som har en periode på 9, bruk en overgang til en annen notasjon av en periodisk brøk med en periode på $0$. Bare for dette formålet erstattes periode 9 med periode $0$, og verdien av det nest høyeste sifferet økes med $1$.
Eksempel 4
For eksempel kan den periodiske brøken $7,45(9)$ erstattes av den periodiske brøken $7,46(0)$ eller den tilsvarende desimalbrøken $7,46$.
Uendelig desimal periodiske brøker er representert med rasjonelle tall. Med andre ord kan enhver periodisk brøk omdannes til en vanlig brøk, og enhver vanlig brøk kan representeres som en periodisk brøk.
Konvertering av brøker til endelige og uendelige periodiske desimaler
Ikke bare vanlige brøker med nevnere $10, 100, \dots$ kan konverteres til en desimalbrøk.
I noen tilfeller kan den opprinnelige fellesbrøken lett reduseres til en nevner på $10$, $100$ eller $1\000$, hvoretter den resulterende brøken kan representeres som en desimalbrøk.
Eksempel 5
For å konvertere brøken $\frac(3)(5)$ til en brøk med nevneren $10$, må du multiplisere telleren og nevneren til brøken med $2$, hvoretter vi får $\frac(6)( 10)$, som ikke er vanskelig å oversette til desimalbrøken $0,6$.
For andre tilfeller brukes en annen metode for å konvertere en vanlig brøk til en desimal):
telleren må erstattes med en desimalbrøk med et hvilket som helst antall nuller etter desimaltegnet;
del telleren av brøken med nevneren (delingen utføres som en deling av naturlige tall i en kolonne, og i kvotienten settes et desimaltegn etter slutten av delingen av hele delen av utbyttet).
Eksempel 6
Konverter brøken $\frac(621)(4)$ til en desimal.
Løsning.
La oss representere tallet $621$ i telleren som en desimalbrøk. For å gjøre dette, legg til et desimaltegn og, for det første, to nuller etter det. Deretter kan du om nødvendig legge til flere nuller. Så vi mottok $621,00$.
La oss dele tallet $621.00$ med $4$ i en kolonne:
Bilde 1.
Divisjonen nådde desimaltegnet i utbyttet, og resten var ikke null. I dette tilfellet plasseres et desimaltegn i kvotienten og divisjonen fortsetter i en kolonne, uavhengig av kommaene:
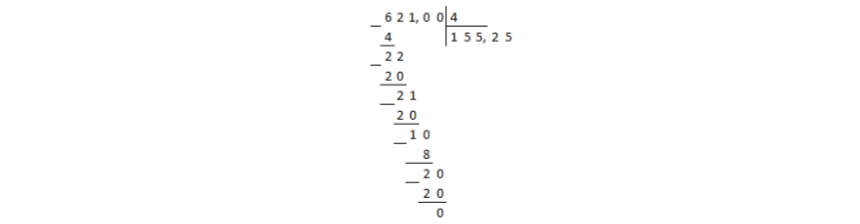
Figur 2.
Resten er null, noe som betyr at delingen er over.
Svar: $155,25$.
Det er mulig at når du deler telleren og nevneren av en vanlig brøk, vil ikke resten resultere i $0$. I dette tilfellet kan delingen fortsette på ubestemt tid. Fra et bestemt øyeblikk gjentas restene fra divisjon periodisk, noe som betyr at tallene i kvotienten også gjentas. Fra dette kan vi konkludere med at denne ordinære brøken vil bli konvertert til en uendelig periodisk desimalbrøk.
Eksempel 7
Konverter brøken $\frac(19)(44)$ til en desimal.
Løsning.)
For å konvertere en vanlig brøk til en desimal, utfør lang divisjon:

Figur 3.
I divisjon gjentas restene $8$ og $36$, og i kvotienten gjentas også tallene $1$ og $8$. Så den opprinnelige ordinære brøken $\frac(19)(44)$ ble konvertert til en periodisk brøk $\frac(19)(44)=0,43181818\dots =0,43(18)$.
Svar: $0,43(18)$.
Generell konklusjon om å konvertere vanlige brøker til desimaler:
hvis nevneren kan dekomponeres til primfaktorer, blant hvilke bare tallene $2$ og $5$ vil være til stede, så kan en slik brøk konverteres til en endelig desimalbrøk;
hvis utvidelsen av nevneren i tillegg til tallene $2$ og $5$ inneholder andre primtall, så konverteres en slik brøk til en uendelig desimal periodisk brøk.

