Cet article est à propos de décimales. Ici, nous comprendrons la notation décimale des nombres fractionnaires, introduirons le concept de fraction décimale et donnerons des exemples de fractions décimales. Nous parlerons ensuite des chiffres des fractions décimales et donnerons les noms des chiffres. Après cela, nous nous concentrerons sur les fractions décimales infinies, parlons des fractions périodiques et non périodiques. Ci-dessous nous listons les principales actions avec décimales. En conclusion, établissons la position des fractions décimales sur la poutre de coordonnées.
Navigation dans les pages.
Notation décimale d'un nombre fractionnaire
Lire des décimales
Disons quelques mots sur les règles de lecture des fractions décimales.
Les fractions décimales, qui correspondent aux fractions ordinaires propres, se lisent de la même manière que ces fractions ordinaires, seul « zéro entier » est d'abord ajouté. Par exemple, la fraction décimale 0,12 correspond à la fraction commune 12/100 (lire « douze centièmes »), donc 0,12 se lit comme « zéro virgule douze centièmes ».
Les fractions décimales qui correspondent aux nombres fractionnaires se lisent exactement de la même manière que ces nombres fractionnaires. Par exemple, la fraction décimale 56,002 correspond à un nombre fractionnaire, donc la fraction décimale 56,002 se lit comme « cinquante-six virgule deux millièmes ».
Places en décimales
En écrivant des fractions décimales, ainsi qu'en écrivant nombres naturels, la signification de chaque chiffre dépend de sa position. En effet, le chiffre 3 dans la fraction décimale 0,3 signifie trois dixièmes, dans la fraction décimale 0,0003 - trois dix millièmes et dans la fraction décimale 30 000,152 - trois dizaines de milliers. Nous pouvons donc en parler décimales, ainsi que sur les chiffres des nombres naturels.
Les noms des chiffres de la fraction décimale jusqu'au point décimal coïncident complètement avec les noms des chiffres des nombres naturels. Et les noms des décimales après la virgule décimale peuvent être vus dans le tableau suivant.

Par exemple, dans la fraction décimale 37,051, le chiffre 3 est à la place des dizaines, 7 à la place des unités, 0 à la place des dixièmes, 5 à la place des centièmes et 1 à la place des millièmes.
Les places dans les fractions décimales diffèrent également par leur priorité. Si en écrivant une fraction décimale nous passons de chiffre en chiffre de gauche à droite, alors nous passerons de personnes âgéesÀ grades juniors. Par exemple, la place des centaines est plus ancienne que la place des dixièmes, et la place des millions est inférieure à la place des centièmes. Dans une fraction décimale finale donnée, on peut parler des chiffres majeurs et mineurs. Par exemple, en fraction décimale 604,9387 senior (le plus élevé) l'endroit est l'endroit des centaines, et junior (le plus bas)- chiffre des dix millièmes.
Pour les fractions décimales, une expansion en chiffres a lieu. C’est similaire à l’expansion en chiffres d’entiers naturels. Par exemple, le développement en décimales de 45,6072 est le suivant : 45,6072=40+5+0,6+0,007+0,0002. Et les propriétés d'addition issues de la décomposition d'une fraction décimale en chiffres permettent de passer à d'autres représentations de cette fraction décimale, par exemple, 45,6072=45+0,6072, ou 45,6072=40,6+5,007+0,0002, ou 45,6072= 45,0072+ 0,6.
Fin des décimales
Jusqu’à présent, nous n’avons parlé que de fractions décimales, dans la notation desquelles il y a un nombre fini de chiffres après la virgule. De telles fractions sont appelées décimales finies.
Définition.
Fin des décimales- Il s'agit de fractions décimales dont les enregistrements contiennent un nombre fini de caractères (chiffres).
Voici quelques exemples de fractions décimales finales : 0,317, 3,5, 51,1020304958, 230 032,45.
Cependant, toutes les fractions ne peuvent pas être représentées sous forme décimale finale. Par exemple, la fraction 5/13 ne peut pas être remplacée par une fraction égale avec l'un des dénominateurs 10, 100, ..., elle ne peut donc pas être convertie en une fraction décimale finale. Nous en parlerons davantage dans la section théorique, sur la conversion de fractions ordinaires en décimales.
Décimales infinies : fractions périodiques et fractions non périodiques
En écrivant une fraction décimale après la virgule, vous pouvez supposer la possibilité d'un nombre infini de chiffres. Dans ce cas, nous en viendrons à considérer les fractions décimales dites infinies.
Définition.
Décimales infinies- Ce sont des fractions décimales contenant un nombre infini de chiffres.
Il est clair que nous ne pouvons pas écrire des fractions décimales infinies sous leur forme complète, donc dans leur enregistrement, nous nous limitons seulement à un certain nombre fini de chiffres après la virgule décimale et mettons des points de suspension indiquant une séquence de chiffres infiniment continue. Voici quelques exemples de fractions décimales infinies : 0,143940932…, 3,1415935432…, 153,02003004005…, 2,111111111…, 69,74152152152….
Si vous regardez attentivement les deux dernières fractions décimales infinies, alors dans la fraction 2,111111111... le nombre 1 qui se répète sans fin est clairement visible, et dans la fraction 69,74152152152..., à partir de la troisième décimale, un groupe de nombres répétitifs 1, 5 et 2 sont clairement visibles. De telles fractions décimales infinies sont appelées périodiques.
Définition.
Décimales périodiques(ou simplement fractions périodiques) sont des fractions décimales sans fin, dans l'enregistrement desquelles, à partir d'une certaine décimale, un nombre ou un groupe de nombres est répété à l'infini, appelé période de la fraction.
Par exemple, la période de la fraction périodique 2,111111111... est le chiffre 1, et la période de la fraction 69,74152152152... est un groupe de chiffres de la forme 152.
Pour les fractions décimales périodiques infinies, il est accepté forme spéciale enregistrements. Par souci de concision, nous avons convenu d'écrire le point une seule fois, en le mettant entre parenthèses. Par exemple, la fraction périodique 2.111111111... s'écrit 2,(1) et la fraction périodique 69.74152152152... s'écrit 69.74(152) .
Il est à noter que pour la même fraction décimale périodique, vous pouvez spécifier différentes périodes. Par exemple, la fraction décimale périodique 0,73333... peut être considérée comme une fraction 0,7(3) de période 3, et aussi comme une fraction 0,7(33) de période 33, et ainsi de suite 0,7(333), 0,7 (3333), ... Vous pouvez aussi regarder la fraction périodique 0,73333 ... comme ceci : 0,733(3), ou comme ceci 0,73(333), etc. Ici, afin d'éviter toute ambiguïté et divergence, nous convenons de considérer comme période d'une fraction décimale la plus courte de toutes les séquences possibles de chiffres répétitifs, et en commençant par la position la plus proche du point décimal. C'est-à-dire que la période de la fraction décimale 0,73333... sera considérée comme une séquence d'un chiffre 3, et la périodicité commence à partir de la deuxième position après la virgule décimale, c'est-à-dire 0,73333...=0,7(3). Autre exemple : la fraction périodique 4,7412121212... a une période de 12, la périodicité commence à partir du troisième chiffre après la virgule, soit 4,7412121212...=4,74(12).
Des fractions périodiques décimales infinies sont obtenues lorsqu'elles sont converties en fractions décimales fractions ordinaires, dont les dénominateurs contiennent des facteurs premiers autres que 2 et 5.
Ici, il convient de mentionner les fractions périodiques avec une période de 9. Donnons des exemples de telles fractions : 6.43(9) , 27,(9) . Ces fractions sont une autre notation pour les fractions périodiques de période 0, et elles sont généralement remplacées par des fractions périodiques de période 0. Pour ce faire, la période 9 est remplacée par la période 0 et la valeur du chiffre le plus élevé suivant est augmentée de un. Par exemple, une fraction de période 9 de la forme 7,24(9) est remplacée par une fraction périodique de période 0 de la forme 7,25(0) ou une fraction décimale finale égale 7,25. Autre exemple : 4,(9)=5,(0)=5. L'égalité d'une fraction de période 9 et de sa fraction correspondante de période 0 s'établit facilement après avoir remplacé ces fractions décimales par des fractions ordinaires égales.
Enfin, examinons de plus près les fractions décimales infinies, qui ne contiennent pas une séquence de chiffres répétitive sans fin. Ils sont dits non périodiques.
Définition.
Décimales non récurrentes(ou simplement fractions non périodiques) sont des fractions décimales infinies qui n’ont pas de point.
Parfois, les fractions non périodiques ont une forme similaire à celle des fractions périodiques, par exemple, 8,02002000200002... est une fraction non périodique. Dans ces cas-là, vous devez être particulièrement attentif à remarquer la différence.
Notez que les fractions non périodiques ne sont pas converties en fractions ordinaires ; les fractions décimales non périodiques infinies représentent des nombres irrationnels.
Opérations avec des décimales
L'une des opérations avec les fractions décimales est la comparaison, et les quatre fonctions arithmétiques de base sont également définies opérations avec des décimales: addition, soustraction, multiplication et division. Considérons séparément chacune des actions avec des fractions décimales.
Comparaison des décimales essentiellement basé sur la comparaison de fractions ordinaires correspondant aux fractions décimales comparées. Cependant, la conversion de fractions décimales en fractions ordinaires est un processus plutôt laborieux, et les fractions non périodiques infinies ne peuvent pas être représentées comme une fraction ordinaire, il est donc pratique d'utiliser une comparaison géographique des fractions décimales. La comparaison géographique des fractions décimales est similaire à la comparaison des nombres naturels. Pour des informations plus détaillées, nous vous recommandons d'étudier l'article : comparaison de fractions décimales, règles, exemples, solutions.
Passons à Prochaine action - multiplier des décimales. La multiplication de fractions décimales finies s'effectue de la même manière que la soustraction de fractions décimales, les règles, les exemples, les solutions à la multiplication par une colonne de nombres naturels. Dans le cas de fractions périodiques, la multiplication peut être réduite à la multiplication de fractions ordinaires. À son tour, la multiplication de fractions décimales non périodiques infinies après leur arrondi se réduit à la multiplication de fractions décimales finies. Nous recommandons pour une étude plus approfondie le matériel de l'article : multiplication de fractions décimales, règles, exemples, solutions.
Décimales sur un rayon de coordonnées
Il existe une correspondance biunivoque entre les points et les décimales.
Voyons comment sont construits les points sur le rayon de coordonnées qui correspondent à une fraction décimale donnée.
Nous pouvons remplacer les fractions décimales finies et les fractions décimales périodiques infinies par des fractions ordinaires égales, puis construire les fractions ordinaires correspondantes sur le rayon de coordonnées. Par exemple, la fraction décimale 1,4 correspond à la fraction commune 14/10, donc le point de coordonnée 1,4 est éloigné de l'origine dans le sens positif de 14 segments égaux à un dixième de segment unitaire.

Les fractions décimales peuvent être marquées sur un rayon de coordonnées, à partir de la décomposition d'une fraction décimale donnée en chiffres. Par exemple, devons construire un point de coordonnée 16.3007, puisque 16.3007=16+0.3+0.0007, alors nous pouvons arriver à ce point en posant séquentiellement 16 segments unitaires à partir de l'origine des coordonnées, 3 segments dont la longueur est égale à un dixième d'une unité, et 7 segments dont la longueur est égale à un dix millième de segment unitaire.
Cette façon de construire Nombres décimaux sur le rayon de coordonnées permet de se rapprocher à volonté du point correspondant à la fraction décimale infinie.
Parfois, il est possible de tracer avec précision le point correspondant à une fraction décimale infinie. Par exemple, ![]() , alors cette fraction décimale infinie 1,41421... correspond à un point du rayon de coordonnées, éloigné de l'origine des coordonnées de la longueur de la diagonale d'un carré de côté de 1 segment unitaire.
, alors cette fraction décimale infinie 1,41421... correspond à un point du rayon de coordonnées, éloigné de l'origine des coordonnées de la longueur de la diagonale d'un carré de côté de 1 segment unitaire.
Le processus inverse d'obtention de la fraction décimale correspondant à un point donné sur un rayon de coordonnées est ce qu'on appelle mesure décimale d'un segment. Voyons comment cela se fait.
Supposons que notre tâche soit d'aller de l'origine à un point donné sur la ligne de coordonnées (ou de s'en approcher à l'infini si nous ne pouvons pas y accéder). Avec la mesure décimale d'un segment, on peut séparer séquentiellement de l'origine un nombre quelconque de segments unitaires, puis des segments dont la longueur est égale à un dixième d'unité, puis des segments dont la longueur est égale à un centième d'unité, etc. En enregistrant le nombre de segments de chaque longueur mis de côté, on obtient la fraction décimale correspondant à un point donné du rayon de coordonnées.
Par exemple, pour arriver au point M dans la figure ci-dessus, vous devez réserver 1 segment unitaire et 4 segments dont la longueur est égale à un dixième d'unité. Ainsi, le point M correspond à la fraction décimale 1,4.
Il est clair que les points du rayon de coordonnées, qui ne peuvent être atteints lors du processus de mesure décimale, correspondent à des fractions décimales infinies.
Bibliographie.
- Mathématiques: cahier de texte pour la 5ème année. enseignement général institutions / N. Ya. Vilenkin, V. I. Zhokhov, A. S. Chesnokov, S. I. Shvartsburd. - 21e éd., effacé. - M. : Mnémosyne, 2007. - 280 pp. : ill. ISBN5-346-00699-0.
- Mathématiques. 6e année : pédagogique. pour l'enseignement général institutions / [N. Ya. Vilenkin et autres]. - 22e éd., rév. - M. : Mnémosyne, 2008. - 288 p. : ill. ISBN978-5-346-00897-2.
- Algèbre: cahier de texte pour la 8ème année. enseignement général institutions / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova] ; édité par S.A. Telyakovsky. - 16e éd. - M. : Éducation, 2008. - 271 p. : je vais. - ISBN978-5-09-019243-9.
- Gusev V.A., Mordkovitch A.G. Mathématiques (un manuel pour ceux qui entrent dans les écoles techniques) : Proc. allocation.- M.; Plus haut école, 1984.-351 p., ill.
Comme on le sait, l'ensemble des nombres rationnels (Q) comprend l'ensemble des nombres entiers (Z), qui à son tour comprend l'ensemble des nombres naturels (N). En plus des nombres entiers, les nombres rationnels incluent les fractions.
Pourquoi alors l’ensemble des nombres rationnels est-il parfois considéré comme des fractions décimales périodiques infinies ? En effet, outre les fractions, ils comprennent également les nombres entiers, ainsi que les fractions non périodiques.
Le fait est que tous les nombres entiers, ainsi que n'importe quelle fraction, peuvent être représentés comme une fraction décimale périodique infinie. Autrement dit, pour tous les nombres rationnels, vous pouvez utiliser la même méthode d’enregistrement.
Comment est représentée une décimale périodique infinie ? Dans celui-ci, un groupe répétitif de nombres après la virgule décimale est placé entre parenthèses. Par exemple, 1,56(12) est une fraction dans laquelle le groupe de chiffres 12 est répété, c'est-à-dire que la fraction a la valeur 1,561212121212... et ainsi de suite à l'infini. Un groupe répétitif de nombres est appelé un point.
Cependant, nous pouvons représenter n’importe quel nombre sous cette forme si nous considérons sa période comme étant le nombre 0, qui se répète également à l’infini. Par exemple, le nombre 2 est identique à 2,00000.... Par conséquent, il peut être écrit comme une fraction périodique infinie, c'est-à-dire 2,(0).
La même chose peut être faite avec n’importe quelle fraction finie. Par exemple:
0,125 = 0,1250000... = 0,125(0)
Cependant, en pratique, ils n'utilisent pas la transformation d'une fraction finie en une fraction périodique infinie. Par conséquent, ils séparent les fractions finies et les fractions périodiques infinies. Ainsi, il est plus correct de dire que les nombres rationnels incluent
- tous les entiers
- fractions finales,
- fractions périodiques infinies.
En même temps, rappelez-vous simplement que les entiers et les fractions finies sont représentables en théorie sous la forme de fractions périodiques infinies.
En revanche, les concepts de fini et fraction infinie applicable aux fractions décimales. En ce qui concerne les fractions, les décimales finies et infinies peuvent être représentées de manière unique sous forme de fraction. Cela signifie que du point de vue des fractions ordinaires, les fractions périodiques et finies sont la même chose. De plus, les nombres entiers peuvent également être représentés sous forme de fraction en imaginant que nous divisons le nombre par 1.
Comment représenter une fraction périodique infinie décimale comme une fraction ordinaire ? L’algorithme le plus couramment utilisé ressemble à ceci :
- Réduisez la fraction pour qu'après la virgule décimale, il n'y ait qu'un point.
- Multipliez une fraction périodique infinie par 10 ou 100 ou ... pour que la virgule décimale se déplace vers la droite d'un point (c'est-à-dire qu'un point finit dans la partie entière).
- Associez la fraction originale (a) à la variable x et la fraction (b) obtenue en multipliant par le nombre N à Nx.
- Soustrayez x de Nx. De b je soustrais a. Autrement dit, ils constituent l’équation Nx – x = b – a.
- Lors de la résolution d’une équation, le résultat est une fraction ordinaire.
Un exemple de conversion d'une fraction décimale périodique infinie en une fraction ordinaire :
x = 1,13333...
10x = 11,3333...
10x * 10 = 11,33333... * 10
100x = 113,3333...
100x – 10x = 113,3333... – 11,3333...
90x = 102
X =
Pour écrire un nombre rationnel m/n sous forme de fraction décimale, vous devez diviser le numérateur par le dénominateur. Dans ce cas, le quotient s’écrit sous forme de fraction décimale finie ou infinie.
Écrire numéro donné comme fraction décimale.
Solution. Divisez le numérateur de chaque fraction dans une colonne par son dénominateur : UN) divisez 6 par 25 ; b) diviser 2 par 3 ; V) divisez 1 par 2, puis ajoutez la fraction résultante à un - la partie entière de ce nombre fractionnaire.

Fractions ordinaires irréductibles dont les dénominateurs ne contiennent pas de facteurs premiers autres que 2 Et 5 , sont écrits sous forme de fraction décimale finale.
DANS Exemple 1 quand UN) dénominateur 25=5,5; quand V) le dénominateur est 2, nous obtenons donc les décimales finales 0,24 et 1,5. Quand b) le dénominateur est 3, donc le résultat ne peut pas être écrit sous forme décimale finie.
Est-il possible, sans division longue, de convertir en fraction décimale une telle fraction ordinaire dont le dénominateur ne contient pas d'autres diviseurs que 2 et 5 ? Voyons cela ! Quelle fraction est appelée décimale et s'écrit sans barre de fraction ? Réponse : fraction de dénominateur 10 ; 100 ; 1000, etc Et chacun de ces nombres est un produit égal nombre de deux et cinq. En fait : 10=2 ·5 ; 100=2 ·5 ·2 ·5 ; 1000=2 ·5 ·2 ·5 ·2 ·5 etc.
Par conséquent, le dénominateur d'une fraction ordinaire irréductible devra être représenté comme le produit de « deux » et « cinq », puis multiplié par 2 et (ou) 5 pour que les « deux » et « cinq » deviennent égaux. Alors le dénominateur de la fraction sera égal à 10 ou 100 ou 1000, etc. Pour garantir que la valeur de la fraction ne change pas, nous multiplions le numérateur de la fraction par le même nombre par lequel nous avons multiplié le dénominateur.
Exprimez les fractions courantes suivantes sous forme décimale :
![]()
Solution. Chacune de ces fractions est irréductible. Factorisons le dénominateur de chaque fraction en facteurs premiers.
20=2·2·5. Conclusion : il manque un « A ».
8=2·2·2. Conclusion : il manque trois « A ».
25=5·5. Conclusion : il manque deux « deux ».

Commentaire. En pratique, ils n'utilisent souvent pas la factorisation du dénominateur, mais posent simplement la question : de combien faut-il multiplier le dénominateur pour que le résultat soit un avec des zéros (10 ou 100 ou 1000, etc.). Et puis le numérateur est multiplié par le même nombre.
Alors, au cas où UN)(exemple 2) à partir du nombre 20, vous pouvez obtenir 100 en multipliant par 5, vous devez donc multiplier le numérateur et le dénominateur par 5.
Quand b)(exemple 2) à partir du nombre 8, le nombre 100 ne sera pas obtenu, mais le nombre 1000 sera obtenu en multipliant par 125. Le numérateur (3) et le dénominateur (8) de la fraction sont multipliés par 125.
Quand V)(exemple 2) à partir de 25 vous obtenez 100 si vous multipliez par 4. Cela signifie que le numérateur 8 doit être multiplié par 4.
Une fraction décimale infinie dans laquelle un ou plusieurs chiffres se répètent invariablement dans la même séquence est appelée périodique sous forme décimale. L’ensemble des chiffres répétitifs est appelé la période de cette fraction. Par souci de concision, la période d’une fraction est écrite une seule fois, entre parenthèses.
Quand b)(exemple 1) il n'y a qu'un seul chiffre répétitif et est égal à 6. Par conséquent, notre résultat 0,66... s'écrira ainsi : 0,(6) . Ils lisent : zéro point, six en période.
S'il y a un ou plusieurs chiffres non répétitifs entre la virgule décimale et le premier point, alors une telle fraction périodique est appelée fraction périodique mixte.
Une fraction commune irréductible dont le dénominateur est avec d'autres le multiplicateur contient un multiplicateur 2 ou 5 , devient mixte fraction périodique.
Écrivez les nombres sous forme de fraction décimale :
![]()
Tout nombre rationnel peut s’écrire sous la forme d’une fraction décimale périodique infinie.
Écrivez les nombres sous forme de fraction périodique infinie.
Rappelez-vous comment, dans la toute première leçon sur les nombres décimaux, j'ai dit qu'il existe des fractions numériques qui ne peuvent pas être représentées sous forme de décimales (voir la leçon « Décimales ») ? Nous avons également appris à factoriser les dénominateurs de fractions pour voir s'il y avait des nombres autres que 2 et 5.
Donc : j'ai menti. Et aujourd'hui, nous allons apprendre à convertir absolument n'importe quelle fraction numérique en décimal. Par la même occasion, nous ferons connaissance avec toute une classe de fractions à partie significative infinie.
Un nombre décimal périodique est un nombre décimal qui :
- La partie significative est constituée d'un nombre infini de chiffres ;
- A certains intervalles, les chiffres de la partie significative sont répétés.
L'ensemble des chiffres répétitifs qui constituent la partie significative est appelé la partie périodique d'une fraction, et le nombre de chiffres de cet ensemble est appelé la période de la fraction. Le segment restant de la partie significative, qui n’est pas répété, est appelé partie non périodique.
Puisqu’il existe de nombreuses définitions, il convient d’examiner quelques-unes de ces fractions en détail :
Cette fraction apparaît le plus souvent dans les problèmes. Partie non périodique : 0 ; partie périodique : 3 ; durée de la période : 1.
Partie non périodique : 0,58 ; partie périodique : 3 ; durée de la période : encore une fois 1.
Partie non périodique : 1 ; partie périodique : 54 ; durée de la période : 2.
Partie non périodique : 0 ; partie périodique : 641025 ; durée de la période : 6. Pour plus de commodité, les parties répétitives sont séparées les unes des autres par un espace - cela n'est pas nécessaire dans cette solution.
Partie non périodique : 3066 ; partie périodique : 6 ; durée de la période : 1.
Comme vous pouvez le constater, la définition d'une fraction périodique repose sur le concept partie importante d'un certain nombre. Par conséquent, si vous avez oublié de quoi il s'agit, je vous recommande de le répéter - voir la leçon "".
Transition vers une fraction décimale périodique
Considérons une fraction ordinaire de la forme a /b. Factorisons son dénominateur en facteurs premiers. Il existe deux options :
- Le développement ne contient que les facteurs 2 et 5. Ces fractions sont facilement converties en décimales - voir la leçon « Décimales ». De telles personnes ne nous intéressent pas ;
- Il y a autre chose dans le développement que 2 et 5. Dans ce cas, la fraction ne peut pas être représentée sous forme décimale, mais elle peut être convertie en valeur décimale périodique.
Pour définir une fraction décimale périodique, vous devez trouver ses parties périodiques et non périodiques. Comment? Convertissez la fraction en fraction impropre, puis divisez le numérateur par le dénominateur à l'aide d'un coin.
Ce qui suit se produira :
- Se séparera en premier partie entière , s'il existe ;
- Il peut y avoir plusieurs nombres après la virgule ;
- Après un moment, les chiffres commenceront répéter.
C'est tout! Les nombres répétitifs après la virgule décimale sont désignés par la partie périodique, et ceux qui précèdent sont désignés par la partie non périodique.
Tâche. Convertissez des fractions ordinaires en décimales périodiques :
Toutes les fractions sans partie entière, on divise donc simplement le numérateur par le dénominateur avec un « coin » :

Comme vous pouvez le constater, les restes se répètent. Écrivons la fraction sous la forme « correcte » : 1,733 ... = 1,7(3).

Le résultat est une fraction : 0,5833 ... = 0,58(3).

Écrire à forme normale: 4,0909 ... = 4,(09).

On obtient la fraction : 0,4141 ... = 0.(41).
Transition de la fraction décimale périodique à la fraction ordinaire
Considérons la fraction décimale périodique X = abc (a 1 b 1 c 1). Il est nécessaire de le transformer en un classique « à deux étages ». Pour ce faire, suivez quatre étapes simples :
- Trouvez la période de la fraction, c'est-à-dire comptez le nombre de chiffres dans la partie périodique. Soit ceci le nombre k ;
- Trouvez la valeur de l'expression X · 10 k. Cela équivaut à décaler la virgule décimale de période complèteà droite - voir la leçon « Multiplier et diviser des nombres décimaux » ;
- L'expression originale doit être soustraite du nombre résultant. Dans ce cas, la partie périodique est « brûlée » et reste fraction commune;
- Trouvez X dans l'équation résultante. Nous convertissons toutes les fractions décimales en fractions ordinaires.
Tâche. Réduire à l'ordinaire fraction impropre Nombres:
- 9,(6);
- 32,(39);
- 0,30(5);
- 0,(2475).
On travaille avec la première fraction : X = 9,(6) = 9,666 ...
Les parenthèses ne contiennent qu'un seul chiffre, donc le point est k = 1. Ensuite, on multiplie cette fraction par 10 k = 10 1 = 10. On a :
10X = 10 9,6666... = 96,666...
Soustrayez la fraction d'origine et résolvez l'équation :
10X − X = 96,666 ... − 9,666 ... = 96 − 9 = 87 ;
9X = 87 ;
X = 87/9 = 29/3.
Examinons maintenant la deuxième fraction. Donc X = 32,(39) = 32,393939...
Période k = 2, donc multipliez le tout par 10 k = 10 2 = 100 :
100X = 100 · 32,393939 ... = 3239,3939 ...
Soustrayez à nouveau la fraction d'origine et résolvez l'équation :
100X − X = 3239,3939 ... − 32,3939 ... = 3239 − 32 = 3207 ;
99X = 3207 ;
X = 3207/99 = 1069/33.
Passons à la troisième fraction : X = 0,30(5) = 0,30555... Le schéma est le même, je vais donc juste donner les calculs :
Période k = 1 ⇒ multiplier le tout par 10 k = 10 1 = 10 ;
10X = 10 0,30555... = 3,05555...
10X − X = 3,0555 ... − 0,305555 ... = 2,75 = 11/4 ;
9X = 11/4 ;
X = (11/4) : 9 = 11/36.
Enfin, la dernière fraction : X = 0,(2475) = 0,2475 2475... Encore une fois, pour plus de commodité, les parties périodiques sont séparées les unes des autres par des espaces. Nous avons:
k = 4 ⇒ 10 k = 10 4 = 10 000 ;
10 000X = 10 000 0,2475 2475 = 2475,2475 ...
10 000X − X = 2475,2475 ... − 0,2475 2475 ... = 2475 ;
9999X = 2475 ;
X = 2475 : 9999 = 25/101.
Décimales infinies
Les décimales après la virgule peuvent contenir un nombre infini de chiffres.
Décimales infinies- ce sont des fractions décimales, qui contiennent un nombre infini de chiffres.
Une fraction décimale infinie est presque impossible à écrire complètement, donc lors de leur écriture, elles sont limitées à seulement un certain nombre fini de chiffres après la virgule décimale, après quoi elles mettent des points de suspension, qui indiquent une séquence de chiffres infiniment continue.
Exemple 1
Par exemple, $0.443340831\dots ; 3.1415935432\points ; 135.126730405\points ; 4.33333333333\points ; 676.68349349\points$.
Regardons les deux dernières décimales infinies. Dans la fraction $4,33333333333\dots$ le chiffre $3$ est répété à l'infini, et dans la fraction $676,68349349\dots$ le groupe de chiffres $3$, $4$ et $9$ est répété à partir de la troisième décimale. De telles fractions décimales infinies sont appelées périodiques.
Décimales périodiques
Décimales périodiques(ou fractions périodiques) sont des fractions décimales infinies, dans l'enregistrement desquelles un nombre ou un groupe de nombres, appelé période de la fraction, est répété sans fin à partir d'une certaine décimale).
Exemple 2
Par exemple, la période de la fraction périodique $4,33333333333\dots$ est le chiffre $3$, et la période de la fraction $676,68349349\dots$ est le groupe de chiffres $349$.
Par souci de concision lors de l'écriture de fractions décimales périodiques infinies, il est d'usage d'écrire le point une fois, en le mettant entre parenthèses. Par exemple, la fraction périodique $4,33333333333\dots$ s'écrit $4,(3)$, et la fraction périodique $676,68349349\dots$ s'écrit $676,68(349)$.
Les fractions décimales périodiques infinies sont obtenues en convertissant des fractions communes dont les dénominateurs contiennent des facteurs premiers autres que 2$ et 5$ en fractions décimales.
Toute fraction décimale finie (et entier) peut être écrite sous forme de fraction périodique en ajoutant un nombre infini de chiffres $0$ à droite.
Exemple 3
Par exemple, le nombre décimal fini $45,12$ pourrait être écrit sous forme de fraction périodique sous la forme $45,12(0)$, et l'entier $(74)$ sous forme de décimale périodique infinie serait $74(0)$.
Dans le cas de fractions périodiques ayant une période de 9, utilisez une transition vers une autre notation d'une fraction périodique avec une période de $0$. Uniquement à cette fin, la période 9 est remplacée par la période $0$ et la valeur du chiffre suivant le plus élevé est augmentée de 1$.
Exemple 4
Par exemple, la fraction périodique $7,45(9)$ peut être remplacée par la fraction périodique $7,46(0)$ ou la fraction décimale équivalente $7,46$.
Les fractions périodiques décimales infinies sont représentées par des nombres rationnels. En d’autres termes, toute fraction périodique peut être convertie en fraction commune, et toute fraction commune peut être représentée comme une fraction périodique.
Conversion de fractions en décimales périodiques finies et infinies
Non seulement les fractions ordinaires avec des dénominateurs $10, 100, \dots$ peuvent être converties en fraction décimale.
Dans certains cas, la fraction commune originale peut être facilement réduite à un dénominateur de 10 $, 100 $ ou 1 000 $, après quoi la fraction résultante peut être représentée sous forme de fraction décimale.
Exemple 5
Pour convertir la fraction $\frac(3)(5)$ en une fraction avec un dénominateur de 10$, vous devez multiplier le numérateur et le dénominateur de la fraction par 2$, après quoi nous obtenons $\frac(6)( 10)$, ce qui n'est pas difficile à traduire en fraction décimale $0,6$.
Pour les autres cas, une autre méthode de conversion d'une fraction commune en décimale est utilisée) :
le numérateur doit être remplacé par une fraction décimale avec n'importe quel nombre de zéros après la virgule décimale ;
divisez le numérateur de la fraction par le dénominateur (la division est effectuée comme une division d'entiers naturels en colonne, et dans le quotient un point décimal est placé après la fin de la division de toute la partie du dividende).
Exemple 6
Convertissez la fraction $\frac(621)(4)$ en décimal.
Solution.
Représentons le nombre $621$ au numérateur sous forme de fraction décimale. Pour ce faire, ajoutez un point décimal et, pour commencer, deux zéros après. Ensuite, si nécessaire, vous pouvez ajouter des zéros supplémentaires. Nous avons donc reçu 621,00$.
Divisons le nombre 621,00$ par 4$ dans une colonne :
Image 1.
La division a atteint la virgule décimale du dividende, et le reste n'était pas nul. Dans ce cas, un point décimal est placé dans le quotient et la division se poursuit dans une colonne, quelles que soient les virgules :
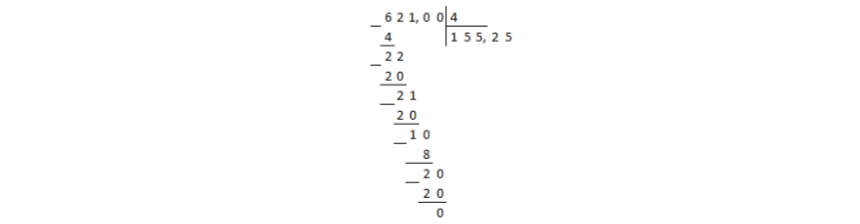
Figure 2.
Le reste est nul, ce qui signifie que la division est terminée.
Répondre: $155,25$.
Il est possible qu'en divisant le numérateur et le dénominateur d'une fraction ordinaire, le reste ne donne pas 0$. Dans ce cas, la division peut se poursuivre indéfiniment. A partir d'un certain moment, les restes de la division se répètent périodiquement, ce qui signifie que les nombres du quotient se répètent également. De là, nous pouvons conclure que cette fraction ordinaire sera convertie en une fraction décimale périodique infinie.
Exemple 7
Convertissez la fraction $\frac(19)(44)$ en décimal.
Solution.)
Pour convertir une fraction commune en décimale, effectuez une division longue :

Figure 3.
Dans la division, les restes $8$ et $36$ sont répétés, et dans le quotient les nombres $1$ et $8$ sont également répétés. Ainsi, la fraction ordinaire originale $\frac(19)(44)$ a été convertie en une fraction périodique $\frac(19)(44)=0,43181818\dots =0,43(18)$.
Répondre: $0,43(18)$.
Conclusion générale sur la conversion de fractions ordinaires en décimales :
si le dénominateur peut être décomposé en facteurs premiers, parmi lesquels seuls les nombres $2$ et $5$ seront présents, alors une telle fraction peut être convertie en une fraction décimale finale ;
si, en plus des nombres $2$ et $5$, le développement du dénominateur contient d'autres nombres premiers, alors une telle fraction est convertie en une fraction périodique décimale infinie.

