Acest articol este despre zecimale. Aici vom înțelege notația zecimală a numerelor fracționale, vom introduce conceptul de fracție zecimală și vom da exemple de fracții zecimale. În continuare, vom vorbi despre cifrele fracțiilor zecimale și vom oferi numele cifrelor. După aceasta, ne vom concentra asupra fracțiilor zecimale infinite, să vorbim despre fracții periodice și neperiodice. Mai jos enumeram principalele actiuni cu zecimale. În concluzie, să stabilim poziția fracțiilor zecimale pe fasciculul de coordonate.
Navigare în pagină.
Notarea zecimală a unui număr fracționar
Citirea zecimale
Să spunem câteva cuvinte despre regulile de citire a fracțiilor zecimale.
Fracțiile zecimale, care corespund fracțiilor ordinare propriu-zise, sunt citite în același mod ca aceste fracții obișnuite, se adaugă mai întâi doar „numărul întreg zero”. De exemplu, fracția zecimală 0,12 corespunde fracției comune 12/100 (a se citi „douăsprezece sutimi”), prin urmare, 0,12 este citit ca „virgul zero douăsprezece sutimi”.
Fracțiile zecimale care corespund numerelor mixte se citesc exact la fel ca aceste numere mixte. De exemplu, fracția zecimală 56,002 corespunde unui număr mixt, astfel încât fracția zecimală 56,002 este citită ca „cincizeci și șase virgulă două miimi”.
Locurile în zecimale
În scrierea fracțiilor zecimale, precum și în scris numere naturale, semnificația fiecărei cifre depinde de poziția sa. Într-adevăr, numărul 3 în fracția zecimală 0,3 înseamnă trei zecimi, în fracția zecimală 0,0003 - trei zece miimi, iar în fracția zecimală 30.000,152 - trei zeci de mii. Deci putem vorbi despre zecimale, precum și despre cifrele din numere naturale.
Numele cifrelor din fracția zecimală până la virgulă coincid complet cu numele cifrelor din numere naturale. Și numele zecimalei după virgulă pot fi văzute din următorul tabel.

De exemplu, în fracția zecimală 37,051, cifra 3 este în locul zecilor, 7 este în locul unităților, 0 este în locul zecimii, 5 este în locul sutimiilor și 1 este în locul miilor.
Locurile din fracțiile zecimale diferă și ca prioritate. Dacă în scrierea unei fracții zecimale trecem de la cifră la cifră de la stânga la dreapta, atunci ne vom muta de la seniori La grade juniori. De exemplu, locul sutelor este mai vechi decât locul zecimii, iar locul milioanelor este mai mic decât locul sutimilor. Într-o fracție zecimală finală dată, putem vorbi despre cifrele majore și minore. De exemplu, în fracția zecimală 604,9387 senior (cel mai înalt) locul este locul sutelor și junior (cel mai mic)- cifra a zece miimii.
Pentru fracțiile zecimale are loc extinderea în cifre. Este similar cu extinderea în cifre ale numerelor naturale. De exemplu, extinderea în zecimale de 45,6072 este următoarea: 45,6072=40+5+0,6+0,007+0,0002. Iar proprietățile de adunare din descompunerea unei fracții zecimale în cifre vă permit să treceți la alte reprezentări ale acestei fracții zecimale, de exemplu, 45.6072=45+0.6072, sau 45.6072=40.6+5.007+0.0002, sau 45.6072=45.6072=45. 0,6.
Încheierea cu zecimale
Până în acest moment, am vorbit doar despre fracții zecimale, în notarea cărora există un număr finit de cifre după virgulă. Astfel de fracții se numesc zecimale finite.
Definiție.
Încheierea cu zecimale- Acestea sunt fracții zecimale, ale căror înregistrări conțin un număr finit de caractere (cifre).
Iată câteva exemple de fracții zecimale finale: 0,317, 3,5, 51,1020304958, 230.032,45.
Cu toate acestea, nu orice fracție poate fi reprezentată ca o zecimală finală. De exemplu, fracția 5/13 nu poate fi înlocuită cu o fracție egală cu unul dintre numitorii 10, 100, ..., prin urmare, nu poate fi convertită într-o fracție zecimală finală. Vom vorbi mai multe despre acest lucru în secțiunea de teorie, conversia fracțiilor obișnuite în zecimale.
Decimale infinite: fracții periodice și fracții neperiodice
Scriind o fracție zecimală după virgulă, puteți presupune posibilitatea unui număr infinit de cifre. În acest caz, vom ajunge să luăm în considerare așa-numitele fracții zecimale infinite.
Definiție.
zecimale infinite- Acestea sunt fracții zecimale, care conțin un număr infinit de cifre.
Este clar că nu putem scrie fracții zecimale infinite în formă completă, așa că în înregistrarea lor ne limităm doar la un anumit număr finit de cifre după virgulă zecimală și punem o elipsă care indică o succesiune infinită de cifre. Iată câteva exemple de fracții zecimale infinite: 0,143940932…, 3,1415935432…, 153,02003004005…, 2,111111111…, 69,74152152152….
Dacă te uiți cu atenție la ultimele două fracții zecimale infinite, atunci în fracția 2,111111111... numărul 1 care se repetă la nesfârșit este vizibil clar, iar în fracția 69,74152152152..., începând cu a treia zecimală, un grup de numere care se repetă 1, 5 și 2 sunt clar vizibile. Astfel de fracții zecimale infinite se numesc periodice.
Definiție.
zecimale periodice(sau pur și simplu fractii periodice) sunt fracții zecimale nesfârșite, în înregistrarea cărora, pornind de la o anumită zecimală, se repetă la nesfârșit un număr sau un grup de numere, care se numește perioada fracției.
De exemplu, perioada fracției periodice 2,111111111... este cifra 1, iar perioada fracției 69,74152152152... este un grup de cifre de forma 152.
Pentru fracții zecimale periodice infinite se acceptă formă specialăînregistrări. Pentru concizie, am convenit să notăm perioada o dată, anexând-o între paranteze. De exemplu, fracția periodică 2,111111111... se scrie ca 2,(1) , iar fracția periodică 69,74152152152... este scrisă ca 69,74(152) .
Este de remarcat faptul că pentru aceeași fracție zecimală periodică puteți specifica perioade diferite. De exemplu, fracția zecimală periodică 0,73333... poate fi considerată ca o fracție 0,7(3) cu o perioadă de 3 și, de asemenea, ca o fracție 0,7(33) cu o perioadă de 33 și așa mai departe 0,7(333), 0,7 (3333), ... De asemenea, puteți privi fracția periodică 0,73333 ... astfel: 0,733(3), sau așa 0,73(333), etc. Aici, pentru a evita ambiguitatea și discrepanțe, suntem de acord să considerăm ca perioadă a unei fracții zecimale cea mai scurtă dintre toate secvențele posibile de cifre repetate, începând de la cea mai apropiată poziție până la punctul zecimal. Adică perioada fracției zecimale 0,73333... va fi considerată o secvență de o cifră 3, iar periodicitatea începe din a doua poziție după virgulă, adică 0,73333...=0,7(3). Un alt exemplu: fracția periodică 4,7412121212... are perioada 12, periodicitatea începe de la a treia cifră după virgulă, adică 4,7412121212...=4,74(12).
Fracțiile periodice zecimale infinite sunt obținute atunci când sunt convertite în fracții zecimale fracții obișnuite, ai căror numitori conțin alți factori primi decât 2 și 5.
Aici merită menționat fracțiile periodice cu o perioadă de 9. Să dăm exemple de astfel de fracții: 6,43(9) , 27,(9) . Aceste fracții sunt o altă notație pentru fracțiile periodice cu perioada 0 și sunt de obicei înlocuite cu fracții periodice cu perioada 0. Pentru a face acest lucru, perioada 9 este înlocuită cu perioada 0, iar valoarea următoarei cifrei cea mai mare este mărită cu unu. De exemplu, o fracție cu perioada 9 de forma 7.24(9) este înlocuită cu o fracție periodică cu perioada 0 de forma 7.25(0) sau o fracție zecimală finală egală 7.25. Un alt exemplu: 4,(9)=5,(0)=5. Egalitatea unei fracții cu perioada 9 și a fracției sale corespunzătoare cu perioada 0 se stabilește ușor după înlocuirea acestor fracții zecimale cu fracții ordinare egale.
În cele din urmă, să aruncăm o privire mai atentă asupra fracțiilor zecimale infinite, care nu conțin o secvență de cifre care se repetă la nesfârșit. Ele sunt numite neperiodice.
Definiție.
zecimale nerecurente(sau pur și simplu fracții neperiodice) sunt fracții zecimale infinite care nu au punct.
Uneori, fracțiile neperiodice au o formă asemănătoare cu cea a fracțiilor periodice, de exemplu, 8,02002000200002... este o fracție neperiodică. În aceste cazuri, ar trebui să fii deosebit de atent să observi diferența.
Rețineți că fracțiile neperiodice nu se convertesc în fracții obișnuite; fracțiile zecimale neperiodice infinite reprezintă numere iraționale.
Operații cu zecimale
Una dintre operațiile cu fracții zecimale este comparația și sunt definite și cele patru funcții aritmetice de bază operatii cu zecimale: adunare, scădere, înmulțire și împărțire. Să luăm în considerare separat fiecare dintre acțiunile cu fracții zecimale.
Comparația zecimale bazată în esență pe compararea fracțiilor obișnuite corespunzătoare fracțiilor zecimale comparate. Cu toate acestea, conversia fracțiilor zecimale în fracții obișnuite este un proces destul de intensiv în muncă, iar fracțiile neperiodice infinite nu pot fi reprezentate ca o fracție obișnuită, așa că este convenabil să folosiți o comparație a fracțiilor zecimale la nivel de loc. Compararea în funcție de locație a fracțiilor zecimale este similară cu compararea numerelor naturale. Pentru informații mai detaliate, vă recomandăm să studiați articolul: comparație de fracții zecimale, reguli, exemple, soluții.
Să trecem la următoarea acțiune - înmulțirea zecimalelor. Înmulțirea fracțiilor zecimale finite se realizează în mod similar cu scăderea fracțiilor zecimale, reguli, exemple, soluții de înmulțire cu o coloană de numere naturale. În cazul fracțiilor periodice, înmulțirea poate fi redusă la înmulțirea fracțiilor obișnuite. La rândul său, înmulțirea fracțiilor zecimale neperiodice infinite după rotunjirea lor se reduce la înmulțirea fracțiilor zecimale finite. Recomandăm pentru studiu în continuare materialul din articol: înmulțirea fracțiilor zecimale, reguli, exemple, soluții.
Decimale pe o rază de coordonate
Există o corespondență unu-la-unu între puncte și zecimale.
Să ne dăm seama cum sunt construite punctele de pe raza de coordonate care corespund unei fracții zecimale date.
Putem înlocui fracții zecimale finite și fracții zecimale periodice infinite cu fracții ordinare egale și apoi construim fracțiile ordinare corespunzătoare pe raza de coordonate. De exemplu, fracția zecimală 1,4 corespunde fracției comune 14/10, deci punctul cu coordonata 1,4 este îndepărtat de la origine în direcția pozitivă cu 14 segmente egale cu o zecime dintr-un segment unitar.

Fracțiile zecimale pot fi marcate pe o rază de coordonate, pornind de la descompunerea unei fracții zecimale date în cifre. De exemplu, trebuie să construim un punct cu coordonata 16.3007, din moment ce 16.3007=16+0.3+0.0007, atunci putem ajunge la acest punct prin așezarea secvențială a 16 segmente unitare de la originea coordonatelor, 3 segmente a căror lungime este egală cu o zecime. dintr-o unitate și 7 segmente, a căror lungime este egală cu o zece miimi dintr-un segment de unitate.
Acest mod de a construi numere zecimale pe raza de coordonate vă permite să vă apropiați cât doriți de punctul corespunzător fracției zecimale infinite.
Uneori este posibil să se traseze cu precizie punctul corespunzător unei fracții zecimale infinite. De exemplu, ![]() , atunci această fracție zecimală infinită 1,41421... corespunde unui punct de pe raza de coordonate, îndepărtat de originea coordonatelor prin lungimea diagonalei unui pătrat cu latura de 1 segment unitar.
, atunci această fracție zecimală infinită 1,41421... corespunde unui punct de pe raza de coordonate, îndepărtat de originea coordonatelor prin lungimea diagonalei unui pătrat cu latura de 1 segment unitar.
Procesul invers de obținere a fracției zecimale corespunzătoare unui punct dat de pe o rază de coordonate este așa-numitul măsurarea zecimală a unui segment. Să ne dăm seama cum se face.
Sarcina noastră să fie să ajungem de la origine la un punct dat pe linia de coordonate (sau să ne apropiem de el la infinit dacă nu putem ajunge la el). Cu măsurarea zecimală a unui segment, putem elimina succesiv de la origine orice număr de segmente de unitate, apoi segmente a căror lungime este egală cu o zecime de unitate, apoi segmente a căror lungime este egală cu o sutime de unitate etc. Înregistrând numărul de segmente din fiecare lungime pusă deoparte, obținem fracția zecimală corespunzătoare unui punct dat de pe raza de coordonate.
De exemplu, pentru a ajunge la punctul M din figura de mai sus, trebuie să lăsați deoparte 1 segment de unitate și 4 segmente, a căror lungime este egală cu o zecime de unitate. Astfel, punctul M corespunde fracției zecimale 1,4.
Este clar că punctele razei de coordonate, care nu pot fi atinse în procesul de măsurare zecimală, corespund unor fracții zecimale infinite.
Bibliografie.
- Matematică: manual pentru clasa a 5-a. educatie generala instituții / N. Ya. Vilenkin, V. I. Zhokhov, A. S. Chesnokov, S. I. Shvartsburd. - Ed. 21, șters. - M.: Mnemosyne, 2007. - 280 p.: ill. ISBN 5-346-00699-0.
- Matematică. Clasa a VI-a: educațională. pentru învăţământul general instituții / [N. Ya. Vilenkin și alții]. - Ed. a 22-a, rev. - M.: Mnemosyne, 2008. - 288 p.: ill. ISBN 978-5-346-00897-2.
- Algebră: manual pentru clasa a VIII-a. educatie generala instituții / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; editat de S. A. Teliakovsky. - Ed. a XVI-a. - M.: Educație, 2008. - 271 p. : bolnav. - ISBN 978-5-09-019243-9.
- Gusev V. A., Mordkovich A. G. Matematică (un manual pentru cei care intră în școlile tehnice): Proc. indemnizatie.- M.; Superior scoala, 1984.-351 p., ill.
După cum se știe, mulțimea numerelor raționale (Q) include mulțimea numerelor întregi (Z), care, la rândul său, include mulțimea numerelor naturale (N). Pe lângă numerele întregi, numerele raționale includ fracții.
Atunci de ce întregul set de numere raționale este uneori considerat fracții zecimale periodice infinite? Într-adevăr, pe lângă fracții, ele includ și numere întregi, precum și fracții neperiodice.
Faptul este că toate numerele întregi, precum și orice fracție, pot fi reprezentate ca o fracție zecimală periodică infinită. Adică, pentru toate numerele raționale puteți folosi aceeași metodă de înregistrare.
Cum este reprezentată o zecimală periodică infinită? În el, un grup repetat de numere după virgulă zecimală este plasat între paranteze. De exemplu, 1,56(12) este o fracție în care grupul de cifre 12 se repetă, adică fracția are valoarea 1,561212121212... și așa mai departe la nesfârșit. Un grup repetat de numere se numește punct.
Cu toate acestea, putem reprezenta orice număr în această formă dacă considerăm că perioada lui este numărul 0, care se repetă și la nesfârșit. De exemplu, numărul 2 este același cu 2,00000.... Prin urmare, poate fi scris ca o fracție periodică infinită, adică 2,(0).
Același lucru se poate face cu orice fracție finită. De exemplu:
0,125 = 0,1250000... = 0,125(0)
Cu toate acestea, în practică nu folosesc transformarea unei fracții finite într-una periodică infinită. Prin urmare, ele separă fracțiile finite și cele periodice infinite. Astfel, este mai corect să spunem că numerele raționale includ
- toate numerele întregi
- fracții finale,
- fracții periodice infinite.
În același timp, pur și simplu amintiți-vă că numerele întregi și fracții finite sunt reprezentabile în teorie sub formă de fracții periodice infinite.
Pe de altă parte, conceptele de finit și fracție infinită aplicabil fracțiilor zecimale. Când vine vorba de fracții, atât zecimale finite, cât și infinite pot fi reprezentate în mod unic ca o fracție. Aceasta înseamnă că din punctul de vedere al fracțiilor obișnuite, fracțiile periodice și finite sunt același lucru. În plus, numerele întregi pot fi reprezentate și ca o fracție imaginându-ne că împărțim numărul la 1.
Cum se reprezintă o fracție periodică infinită zecimală ca o fracție obișnuită? Algoritmul cel mai des folosit este ceva de genul acesta:
- Reduceți fracția astfel încât după virgulă să existe doar o perioadă.
- Înmulțiți o fracție periodică infinită cu 10 sau 100 sau ... astfel încât punctul zecimal să se miște la dreapta cu o perioadă (adică, o perioadă se termină în întreaga parte).
- Echivalează fracția inițială (a) cu variabila x și fracția (b) obținută prin înmulțirea cu numărul N la Nx.
- Scădeți x din Nx. Din b scad a. Adică ele alcătuiesc ecuația Nx – x = b – a.
- La rezolvarea unei ecuații, rezultatul este o fracție obișnuită.
Un exemplu de conversie a unei fracții zecimale periodice infinite într-o fracție obișnuită:
x = 1,13333...
10x = 11,3333...
10x * 10 = 11,33333... * 10
100x = 113,3333...
100x – 10x = 113,3333... – 11,3333...
90x = 102
x =
Pentru a scrie un număr rațional m/n ca fracție zecimală, trebuie să împărțiți numărătorul la numitor. În acest caz, câtul este scris ca o fracție zecimală finită sau infinită.
Scrie număr dat ca fracție zecimală.
Soluţie. Împărțiți numărătorul fiecărei fracții într-o coloană la numitorul ei: A)împărțiți 6 la 25; b)împărțiți 2 la 3; V)împărțiți 1 la 2 și apoi adăugați fracția rezultată la unu - partea întreagă a acestui număr mixt.

Fracții ordinare ireductibile ai căror numitori nu conțin alți factori primi decât 2 Și 5 , sunt scrise ca o fracție zecimală finală.
ÎN exemplu 1 când A) numitorul 25=5·5; când V) numitorul este 2, deci obținem zecimale finale 0,24 și 1,5. Când b) numitorul este 3, deci rezultatul nu poate fi scris ca o zecimală finită.
Este posibil, fără împărțire lungă, să se transforme într-o fracție zecimală o astfel de fracție obișnuită, al cărei numitor nu conține alți divizori decât 2 și 5? Să ne dăm seama! Ce fracție se numește zecimală și se scrie fără bară de fracții? Răspuns: fracția cu numitorul 10; 100; 1000 etc. Și fiecare dintre aceste numere este un produs egal număr de doi și cinci. De fapt: 10=2 ·5 ; 100=2 ·5 ·2 ·5; 1000=2 ·5 ·2 ·5 ·2 ·5 etc.
În consecință, numitorul unei fracții ordinare ireductibile va trebui reprezentat ca produsul dintre „doi” și „cinci”, apoi înmulțit cu 2 și (sau) 5, astfel încât „doi” și „cinci” să devină egali. Atunci numitorul fracției va fi egal cu 10 sau 100 sau 1000 etc. Pentru a ne asigura că valoarea fracției nu se modifică, înmulțim numărătorul fracției cu același număr cu care am înmulțit numitorul.
Exprimați următoarele fracții comune sub formă de zecimale:
![]()
Soluţie. Fiecare dintre aceste fracții este ireductibilă. Să factorăm numitorul fiecărei fracții în factori primi.
20=2·2·5. Concluzie: lipsește un „A”.
8=2·2·2. Concluzie: lipsesc trei „A”.
25=5·5. Concluzie: lipsesc doi „doi”.

Cometariu.În practică, adesea nu folosesc factorizarea numitorului, ci pur și simplu pun întrebarea: cu cât trebuie înmulțit numitorul, astfel încât rezultatul să fie unul cu zerouri (10 sau 100 sau 1000 etc.). Și apoi numărătorul este înmulțit cu același număr.
Deci, în caz A)(exemplul 2) din numărul 20 puteți obține 100 înmulțind cu 5, prin urmare, trebuie să înmulțiți numărătorul și numitorul cu 5.
Când b)(exemplul 2) din numărul 8 nu se va obține numărul 100, dar numărul 1000 se obține prin înmulțirea cu 125. Atât numărătorul (3) cât și numitorul (8) al fracției se înmulțesc cu 125.
Când V)(exemplul 2) de la 25 obțineți 100 dacă înmulțiți cu 4. Aceasta înseamnă că numărătorul 8 trebuie înmulțit cu 4.
Se numește o fracție zecimală infinită în care una sau mai multe cifre se repetă invariabil în aceeași succesiune periodic ca zecimală. Setul de cifre care se repetă se numește perioada acestei fracții. Pentru concizie, perioada unei fracții se scrie o singură dată, cuprinsă între paranteze.
Când b)(exemplul 1) există o singură cifră care se repetă și este egală cu 6. Prin urmare, rezultatul nostru 0,66... va fi scris astfel: 0,(6) . S-au citit: zero punct, șase în punct.
Dacă există una sau mai multe cifre care nu se repetă între punctul zecimal și prima perioadă, atunci o astfel de fracție periodică se numește fracție periodică mixtă.
O fracție comună ireductibilă al cărei numitor este impreuna cu altii multiplicatorul conține multiplicatorul 2 sau 5 , devine amestecat fracție periodică.
Scrieți numerele ca fracție zecimală:
![]()
Orice număr rațional poate fi scris ca o fracție zecimală periodică infinită.
Scrieți numerele ca o fracție periodică infinită.
Vă amintiți cum în prima lecție despre zecimale am spus că există fracții numerice care nu pot fi reprezentate ca zecimale (vezi lecția „Decimale”)? De asemenea, am învățat cum să factorăm numitorii fracțiilor pentru a vedea dacă există alte numere decât 2 și 5.
Deci: am mințit. Și astăzi vom învăța cum să convertim absolut orice fracție numerică într-o zecimală. În același timp, ne vom familiariza cu o întreagă clasă de fracții cu o parte semnificativă infinită.
O zecimală periodică este orice zecimală care:
- Partea semnificativă este formată dintr-un număr infinit de cifre;
- La anumite intervale, numerele din partea semnificativă se repetă.
Setul de cifre care se repetă care alcătuiesc partea semnificativă se numește partea periodică a fracției, iar numărul de cifre din această mulțime se numește perioada fracției. Segmentul rămas al părții semnificative, care nu se repetă, se numește partea neperiodică.
Deoarece există multe definiții, merită să luăm în considerare câteva dintre aceste fracții în detaliu:
Această fracție apare cel mai adesea în probleme. Partea neperiodică: 0; parte periodică: 3; durata perioadei: 1.
Partea neperiodică: 0,58; parte periodică: 3; durata perioadei: din nou 1.
Partea neperiodică: 1; parte periodică: 54; durata perioadei: 2.
Partea neperiodică: 0; piesa periodica: 641025; lungimea perioadei: 6. Pentru comoditate, părțile care se repetă sunt separate între ele printr-un spațiu - acest lucru nu este necesar în această soluție.
Partea neperiodică: 3066; parte periodică: 6; durata perioadei: 1.
După cum puteți vedea, definiția unei fracții periodice se bazează pe concept parte semnificativă a unui număr. Prin urmare, dacă ați uitat ce este, vă recomand să o repetați - vedeți lecția „”.
Trecerea la fracția zecimală periodică
Se consideră o fracție obișnuită de forma a /b. Să factorizăm numitorul său în factori primi. Există două opțiuni:
- Expansiunea conține doar factorii 2 și 5. Aceste fracții sunt ușor convertite în zecimale - vezi lecția „Decimale”. Nu ne interesează astfel de oameni;
- Există și altceva în expansiune, în afară de 2 și 5. În acest caz, fracția nu poate fi reprezentată ca zecimală, dar poate fi convertită într-o zecimală periodică.
Pentru a defini o fracție zecimală periodică, trebuie să găsiți părțile sale periodice și neperiodice. Cum? Convertiți fracția într-o fracție improprie și apoi împărțiți numărătorul la numitor folosind un colț.
Se vor întâmpla următoarele:
- Se va despărți primul întreaga parte , dacă există;
- Pot exista mai multe numere după virgulă zecimală;
- După un timp, numerele vor începe repeta.
Asta e tot! Numerele care se repetă după virgulă sunt notate cu partea periodică, iar cele din față sunt notate cu partea neperiodică.
Sarcină. Convertiți fracțiile obișnuite în zecimale periodice:
Toate fracțiile fără o parte întreagă, așa că pur și simplu împărțim numărătorul la numitorul cu un „colț”:

După cum puteți vedea, restul se repetă. Să scriem fracția în forma „corectă”: 1,733 ... = 1,7(3).

Rezultatul este o fracție: 0,5833 ... = 0,58(3).

Scrie la forma normala: 4,0909 ... = 4,(09).

Obținem fracția: 0,4141 ... = 0.(41).
Trecerea de la fracția zecimală periodică la fracția obișnuită
Se consideră fracția zecimală periodică X = abc (a 1 b 1 c 1). Este necesar să îl convertiți într-unul clasic „cu două etaje”. Pentru a face acest lucru, urmați patru pași simpli:
- Aflați perioada fracției, adică numără câte cifre sunt în partea periodică. Fie acesta numărul k;
- Aflați valoarea expresiei X · 10 k. Acest lucru este echivalent cu deplasarea punctului zecimal cu perioada intreagaîn dreapta - vezi lecția „Înmulțirea și împărțirea zecimalelor”;
- Expresia originală trebuie scăzută din numărul rezultat. În acest caz, partea periodică este „arsă” și rămâne fracție comună;
- Găsiți X în ecuația rezultată. Convertim toate fracțiile zecimale în fracții obișnuite.
Sarcină. Reduceți la obișnuit fracție improprie numere:
- 9,(6);
- 32,(39);
- 0,30(5);
- 0,(2475).
Lucrăm cu prima fracție: X = 9,(6) = 9,666 ...
Parantezele conțin doar o cifră, deci perioada este k = 1. În continuare, înmulțim această fracție cu 10 k = 10 1 = 10. Avem:
10X = 10 9,6666... = 96,666...
Scădeți fracția inițială și rezolvați ecuația:
10X − X = 96,666 ... − 9,666 ... = 96 − 9 = 87;
9X = 87;
X = 87/9 = 29/3.
Acum să ne uităm la a doua fracție. Deci X = 32,(39) = 32,393939...
Perioada k = 2, deci înmulțiți totul cu 10 k = 10 2 = 100:
100X = 100 · 32,393939 ... = 3239,3939 ...
Scădeți din nou fracția inițială și rezolvați ecuația:
100X − X = 3239,3939 ... − 32,3939 ... = 3239 − 32 = 3207;
99X = 3207;
X = 3207/99 = 1069/33.
Să trecem la a treia fracție: X = 0,30(5) = 0,30555... Diagrama este aceeași, așa că voi da doar calculele:
Perioada k = 1 ⇒ înmulțiți totul cu 10 k = 10 1 = 10;
10X = 10 0,30555... = 3,05555...
10X − X = 3,0555 ... − 0,305555 ... = 2,75 = 11/4;
9X = 11/4;
X = (11/4) : 9 = 11/36.
În sfârșit, ultima fracție: X = 0,(2475) = 0,2475 2475... Din nou, pentru comoditate, părțile periodice sunt separate între ele prin spații. Avem:
k = 4 ⇒ 10 k = 10 4 = 10.000;
10.000X = 10.000 0,2475 2475 = 2475,2475 ...
10.000X − X = 2475,2475 ... − 0,2475 2475 ... = 2475;
9999X = 2475;
X = 2475: 9999 = 25/101.
zecimale infinite
Decimale după virgulă zecimală pot conține un număr infinit de cifre.
zecimale infinite- acestea sunt fracții zecimale, care conțin un număr infinit de cifre.
O fracție zecimală infinită este aproape imposibil de scris complet, așa că atunci când le scriu, acestea sunt limitate doar la un anumit număr finit de cifre după virgulă zecimală, după care pun o elipsă, ceea ce indică o succesiune infinită de cifre.
Exemplul 1
De exemplu, $0,443340831\dots ; 3,1415935432\dots ; 135,126730405\dots ; 4,33333333333\dots ; 676,68349349\dots$.
Să ne uităm la ultimele două zecimale infinite. În fracția $4.33333333333\dots$ cifra $3$ se repetă la nesfârșit, iar în fracția $676.68349349\dots$ grupul de cifre $3$, $4$ și $9$ se repetă de la a treia zecimală. Astfel de fracții zecimale infinite se numesc periodice.
zecimale periodice
zecimale periodice(sau fractii periodice) sunt fracții zecimale infinite, în înregistrarea cărora un număr sau un grup de numere, numit perioada fracției, se repetă la nesfârșit de la o anumită zecimală).
Exemplul 2
De exemplu, perioada fracției periodice $4,33333333333\dots$ este cifra $3$, iar perioada fracției $676,68349349\dots$ este grupul de cifre $349$.
Pentru concizie în scrierea fracțiilor zecimale periodice infinite, se obișnuiește să scrieți punctul o dată, încadrându-l între paranteze. De exemplu, fracția periodică $4,33333333333\dots$ este scrisă $4,(3)$, iar fracția periodică $676,68349349\dots$ este scrisă $676,68(349)$.
Fracțiile zecimale periodice infinite sunt obținute prin conversia fracțiilor comune ai căror numitori conțin factori primi, alții decât $2$ și $5$, în fracții zecimale.
Orice fracție zecimală finită (și întreg) poate fi scrisă ca o fracție periodică prin adăugarea unui număr infinit de cifre $0$ la dreapta.
Exemplul 3
De exemplu, zecimala finită $45,12$ ar putea fi scrisă ca o fracție periodică ca $45,12(0)$, iar întregul $(74)$ ca zecimală periodică infinită ar fi $74(0)$.
În cazul fracțiilor periodice care au o perioadă de 9, utilizați o tranziție la o altă notație a unei fracții periodice cu o perioadă de $0$. Doar în acest scop, perioada 9 este înlocuită cu perioada $0$, iar valoarea următoarei cifrei mai mari este mărită cu $1$.
Exemplul 4
De exemplu, fracția periodică $7,45(9)$ poate fi înlocuită cu fracția periodică $7,46(0)$ sau cu fracția zecimală echivalentă $7,46$.
Fracțiile periodice zecimale infinite sunt reprezentate prin numere raționale. Cu alte cuvinte, orice fracție periodică poate fi convertită într-o fracție comună și orice fracție comună poate fi reprezentată ca o fracție periodică.
Conversia fracțiilor în zecimale periodice finite și infinite
Nu numai fracțiile obișnuite cu numitori $10, 100, \dots$ pot fi convertite într-o fracție zecimală.
În unele cazuri, fracția comună inițială poate fi ușor redusă la un numitor de $10$, $100$ sau $1\000$, după care fracția rezultată poate fi reprezentată ca o fracție zecimală.
Exemplul 5
Pentru a converti fracția $\frac(3)(5)$ într-o fracție cu numitorul de $10$, trebuie să înmulțiți numărătorul și numitorul fracției cu $2$, după care obținem $\frac(6)( 10)$, care nu este greu de tradus în fracția zecimală $0,6$.
Pentru alte cazuri, se folosește o altă metodă de conversie a unei fracții comune într-o zecimală):
numărătorul trebuie înlocuit cu o fracție zecimală cu orice număr de zerouri după virgulă;
împărțiți numărătorul fracției la numitor (împărțirea se face ca o împărțire a numerelor naturale într-o coloană, iar în cât se pune un punct zecimal după sfârșitul împărțirii întregii părți a dividendului).
Exemplul 6
Convertiți fracția $\frac(621)(4)$ într-o zecimală.
Soluţie.
Să reprezentăm numărul $621$ la numărător ca o fracție zecimală. Pentru a face acest lucru, adăugați un punct zecimal și, pentru început, două zerouri după acesta. Apoi, dacă este necesar, puteți adăuga mai multe zerouri. Deci, am primit 621,00 USD.
Să împărțim numărul $621.00$ la $4$ într-o coloană:
Poza 1.
Diviziunea a atins punctul zecimal al dividendului, iar restul nu a fost zero. În acest caz, un punct zecimal este plasat în cât și împărțirea continuă într-o coloană, indiferent de virgule:
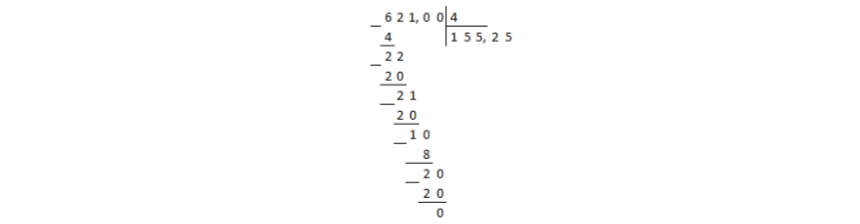
Figura 2.
Restul este zero, ceea ce înseamnă că împărțirea sa încheiat.
Răspuns: $155,25$.
Este posibil ca la împărțirea numărătorului și numitorului unei fracții obișnuite, restul să nu rezulte în $0$. În acest caz, împărțirea poate fi continuată pe termen nelimitat. Începând de la un moment dat, resturile din împărțire se repetă periodic, ceea ce înseamnă că se repetă și numerele din coeficient. Din aceasta putem concluziona că această fracție obișnuită va fi convertită într-o fracție zecimală periodică infinită.
Exemplul 7
Convertiți fracția $\frac(19)(44)$ într-o zecimală.
Soluţie.)
Pentru a converti o fracție comună într-o zecimală, efectuați împărțirea lungă:

Figura 3.
În împărțire se repetă restul $8$ și $36$, iar în cât se repetă și numerele $1$ și $8$. Deci, fracția ordinară originală $\frac(19)(44)$ a fost convertită într-o fracție periodică $\frac(19)(44)=0,43181818\dots =0,43(18)$.
Răspuns: $0,43(18)$.
Concluzie generală despre transformarea fracțiilor obișnuite în zecimale:
dacă numitorul poate fi descompus în factori primi, printre care vor fi prezente doar numerele $2$ și $5$, atunci o astfel de fracție poate fi convertită într-o fracție zecimală finală;
dacă, pe lângă numerele $2$ și $5$, extinderea numitorului conține și alte numere prime, atunci o astfel de fracție este convertită într-o fracție periodică zecimală infinită.

