The concept of the midline of the trapezoid
First, let's remember what figure is called a trapezoid.
Definition 1
A trapezoid is a quadrilateral in which two sides are parallel and the other two are not parallel.
In this case, parallel sides are called the bases of the trapezoid, and not parallel - the sides of the trapezoid.
Definition 2
The midline of a trapezoid is a line segment that connects the midpoints of the sides of the trapezoid.
Trapezium midline theorem
We now introduce the theorem on the midline of a trapezoid and prove it by the vector method.
Theorem 1
The median line of the trapezoid is parallel to the bases and equal to half their sum.
Proof.
Let us be given a trapezoid $ABCD$ with bases $AD\ and\ BC$. And let $MN$ be the midline of this trapezoid (Fig. 1).
Figure 1. The middle line of the trapezoid
Let us prove that $MN||AD\ and\ MN=\frac(AD+BC)(2)$.
Consider the vector $\overrightarrow(MN)$. Next, we use the polygon rule for vector addition. On the one hand, we get that
On the other side
Adding the last two equalities, we get
Since $M$ and $N$ are the midpoints of the sides of the trapezoid, we have
We get:
Hence
From the same equality (since $\overrightarrow(BC)$ and $\overrightarrow(AD)$ are codirectional and, therefore, collinear), we get that $MN||AD$.
The theorem has been proven.
Examples of tasks on the concept of the midline of a trapezoid
Example 1
The sides of the trapezoid are $15\cm$ and $17\cm$ respectively. The perimeter of the trapezoid is $52\cm$. Find the length of the midline of the trapezoid.
Solution.
Denote the midline of the trapezoid by $n$.
The sum of the sides is
Therefore, since the perimeter is $52\ cm$, the sum of the bases is
Hence, by Theorem 1, we obtain
Answer:$10\cm$.
Example 2
The ends of the circle's diameter are $9$ cm and $5$ cm respectively from its tangent. Find the diameter of this circle.
Solution.
Let us be given a circle with center $O$ and diameter $AB$. Draw the tangent $l$ and construct the distances $AD=9\ cm$ and $BC=5\ cm$. Let's draw the radius $OH$ (Fig. 2).

Figure 2.
Since $AD$ and $BC$ are the distances to the tangent, then $AD\bot l$ and $BC\bot l$ and since $OH$ is the radius, then $OH\bot l$, hence $OH |\left|AD\right||BC$. From all this we get that $ABCD$ is a trapezoid, and $OH$ is its midline. By Theorem 1, we get
A quadrilateral with only two parallel sides is called trapeze.
The parallel sides of a trapezoid are called its grounds, and those sides that are not parallel are called sides. If the sides are equal, then such a trapezoid is isosceles. The distance between the bases is called the height of the trapezoid.
Middle line of the trapezium
The median line is a segment connecting the midpoints of the sides of the trapezoid. The midline of a trapezoid is parallel to its bases.
Theorem:
If a line intersecting the middle of one side is parallel to the bases of the trapezoid, then it bisects the second side of the trapezoid.
Theorem:
The length of the midline is equal to the arithmetic mean of the lengths of its bases
MN || AB || DCAM=MD; BN=NC
MN midline, AB and CD - bases, AD and BC - sides
MN=(AB+DC)/2
Theorem:
The length of the midline of a trapezoid is equal to the arithmetic mean of the lengths of its bases.
The main task: Prove that the midline of a trapezoid bisects a segment whose ends lie in the middle of the bases of the trapezoid.
Middle Line of the Triangle
The line segment connecting the midpoints of the two sides of a triangle is called the midline of the triangle. It is parallel to the third side and its length is half the length of the third side.
Theorem: If a line intersecting the midpoint of one side of a triangle is parallel to the other side of the given triangle, then it bisects the third side.

AM = MC and BN = NC =>
Applying Triangle and Trapezoid Midline Properties
The division of a segment into a certain number of equal parts.
Task: Divide segment AB into 5 equal parts.
Solution:
Let p be a random ray whose origin is point A and which does not lie on line AB. We sequentially set aside 5 equal segments on p AA 1 = A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 A 5
We connect A 5 to B and draw lines through A 4 , A 3 , A 2 and A 1 that are parallel to A 5 B. They intersect AB at B 4 , B 3 , B 2 and B 1 respectively. These points divide segment AB into 5 equal parts. Indeed, from the trapezoid BB 3 A 3 A 5 we see that BB 4 = B 4 B 3 . In the same way, from the trapezoid B 4 B 2 A 2 A 4 we get B 4 B 3 = B 3 B 2
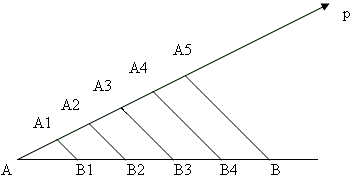
While from the trapezoid B 3 B 1 A 1 A 3 , B 3 B 2 = B 2 B 1 .
Then from B 2 AA 2 it follows that B 2 B 1 = B 1 A. In conclusion, we get:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
It is clear that in order to divide the segment AB into another number of equal parts, we need to project the same number of equal segments onto the ray p. And then continue in the manner described above.
In this article, another selection of tasks with a trapezoid has been made for you. Conditions are somehow connected with its middle line. Task types are taken from the open bank of typical tasks. If you wish, you can refresh your theoretical knowledge. The blog has already covered tasks whose conditions are associated with, as well as. Briefly about the middle line:

The middle line of the trapezoid connects the midpoints of the sides. It is parallel to the bases and equal to their half-sum.
Before solving problems, let's consider a theoretical example.
Given a trapezoid ABCD. The diagonal AC intersecting with the midline forms point K, the diagonal BD forms point L. Prove that the segment KL is equal to half the difference of the bases.

Let's first note the fact that the midline of a trapezoid bisects any segment whose ends lie on its bases. This conclusion suggests itself. Imagine a segment connecting two points of the bases, it will split this trapezoid into two others. It turns out that a segment parallel to the bases of the trapezoid and passing through the middle of the side on the other side will pass through its middle.
It is also based on the Thales theorem:
If on one of the two straight lines several equal segments are sequentially laid aside and parallel lines are drawn through their ends, intersecting the second straight line, then they will cut off equal segments on the second straight line.
That is, in this case, K is the middle of AC and L is the middle of BD. Hence EK is the midline of triangle ABC, LF is the midline of triangle DCB. According to the property of the midline of a triangle:

We can now express the segment KL in terms of bases:
Proven!
This example is not just given. In tasks for independent solution, there is just such a task. Only it does not say that the segment connecting the midpoints of the diagonals lies on the midline. Consider the tasks:
27819. Find the midline of a trapezoid if its bases are 30 and 16.

We calculate by the formula:

27820. The midline of the trapezoid is 28 and the smaller base is 18. Find the larger base of the trapezoid.

Let's express the larger base:
In this way:
27836. A perpendicular dropped from the apex of an obtuse angle to the greater base of an isosceles trapezoid divides it into parts having lengths 10 and 4. Find the midline of this trapezoid.

In order to find the middle line, you need to know the bases. The base AB is easy to find: 10+4=14. Find DC.
Let's construct the second perpendicular DF:

Segments AF, FE and EB will be equal to 4, 6 and 4 respectively. Why?
In an isosceles trapezoid, the perpendiculars dropped to the larger base divide it into three segments. Two of them, which are the legs of cut off right-angled triangles, are equal to each other. The third segment is equal to the smaller base, since when constructing the indicated heights, a rectangle is formed, and in the rectangle, the opposite sides are equal. In this task:

Thus DC=6. We calculate:

27839. The bases of the trapezoid are in ratio 2:3, and the midline is 5. Find the smaller base.

Let's introduce the coefficient of proportionality x. Then AB=3x, DC=2x. We can write:
Therefore, the smaller base is 2∙2=4.
27840. The perimeter of an isosceles trapezoid is 80, its midline is equal to the lateral side. Find the side of the trapezoid.

Based on the condition, we can write:
If we denote the middle line through x, we get:

The second equation can already be written as:

27841. The midline of the trapezoid is 7, and one of its bases is 4 more than the other. Find the larger base of the trapezoid.

Let's denote the smaller base (DC) as x, then the larger one (AB) will be equal to x + 4. We can record
We got that the smaller base is early than five, which means that the larger one is equal to 9.
27842. The midline of the trapezoid is 12. One of the diagonals divides it into two segments, the difference of which is 2. Find the larger base of the trapezoid.

We can easily find the larger base of the trapezoid if we calculate the segment EO. It is the middle line in triangle ADB, and AB=2∙EO.
What do we have? It is said that the middle line is equal to 12 and the difference between the segments EO and OF is equal to 2. We can write down two equations and solve the system:
![]()
It is clear that in this case it is possible to select a pair of numbers without calculations, these are 5 and 7. But, nevertheless, we will solve the system:

So EO=12–5=7. Thus, the larger base is equal to AB=2∙EO=14.
27844. In an isosceles trapezoid, the diagonals are perpendicular. The height of the trapezoid is 12. Find its midline.

Immediately, we note that the height drawn through the intersection point of the diagonals in an isosceles trapezoid lies on the axis of symmetry and divides the trapezoid into two equal rectangular trapezoids, that is, the bases of this height are divided in half.
It would seem that in order to calculate the average line, we must find the grounds. Here a small dead end arises ... How, knowing the height, in this case, calculate the bases? And no how! Many such trapezoids with a fixed height and diagonals intersecting at an angle of 90 degrees can be built. How to be?
Look at the formula for the midline of a trapezoid. After all, we do not need to know the bases themselves, it is enough to know their sum (or half-sum). This we can do.
Since the diagonals intersect at right angles, isosceles right triangles are formed with height EF:
It follows from the above that FO=DF=FC, and OE=AE=EB. Now let's write down what the height expressed through the segments DF and AE is equal to:

So the middle line is 12.
* In general, this is a problem, as you understand, for an oral account. But I'm sure the detailed explanation provided is necessary. And so ... If you look at the figure (provided that the angle between the diagonals is observed during construction), the equality FO=DF=FC, and OE=AE=EB immediately catches your eye.
As part of the prototypes, there are also types of tasks with trapezoids. It was built on a sheet in a cell and it is required to find the middle line, the side of the cell is usually 1, but there may be another value.
27848. Find the midline of the trapezoid ABCD if the sides of the square cells are 1.

It's simple, we calculate the bases by cells and use the formula: (2 + 4) / 2 = 3
If the bases are built at an angle to the cell grid, then there are two ways. For instance!
Lesson Objectives:
1) introduce students to the concept of the midline of a trapezoid, consider its properties and prove them;
2) teach how to build the middle line of the trapezoid;
3) to develop the ability of students to use the definition of the middle line of the trapezoid and the properties of the middle line of the trapezoid when solving problems;
4) continue to develop students' ability to speak correctly, using the necessary mathematical terms; prove your point of view;
5) develop logical thinking, memory, attention.
During the classes
1. Checking homework takes place during the lesson. Homework was oral, remember:
a) definition of a trapezoid; types of trapezium;
b) determination of the midline of the triangle;
c) property of the midline of a triangle;
d) a sign of the midline of the triangle.
2. Learning new material.
a) The trapezoid ABCD is shown on the board.
b) The teacher offers to remember the definition of a trapezoid. Each desk has a hint diagram that helps to remember the basic concepts in the topic “Trapezoid” (see Appendix 1). Appendix 1 is issued for each desk.
Students draw the trapezoid ABCD in their notebook.
c) The teacher suggests recalling in which topic the concept of the middle line was encountered (“The middle line of the triangle”). Students recall the definition of the midline of a triangle and its property.
e) Write down the definition of the midline of the trapezoid, depicting it in a notebook.
middle line A trapezoid is called a segment connecting the midpoints of its sides.
The property of the median line of the trapezoid at this stage remains unproven, so the next stage of the lesson involves working on the proof of the property of the median line of the trapezoid.
Theorem. The midline of a trapezoid is parallel to its bases and equal to half their sum.

Given: ABCD - trapezoid,
MN - middle line ABCD
Prove, what:
1. BC || MN || AD.
2. MN = (AD + BC).
We can write down some corollaries following from the conditions of the theorem:
AM=MB, CN=ND, BC || AD.
It is impossible to prove what is required on the basis of the listed properties alone. The system of questions and exercises should lead students to the desire to connect the midline of a trapezoid with the midline of some triangle, the properties of which they already know. If there are no proposals, then we can ask the question: how to construct a triangle for which the segment MN would be the midline?
Let us write an additional construction for one of the cases.
Let us draw a line BN intersecting the extension of side AD at point K.

Additional elements appear - triangles: ABD, BNM, DNK, BCN. If we prove that BN = NK, then this will mean that MN is the midline of ABD, and then we can use the property of the midline of a triangle and prove the necessary.
Proof:
1. Consider BNC and DNK, in them:
a) CNB =DNK (property of vertical angles);
b) BCN = NDK (property of internal cross lying angles);
c) CN = ND (by the corollary of the hypothesis of the theorem).
So BNC = DNK (on the side and two corners adjacent to it).
Q.E.D.
The proof can be carried out orally in the lesson, and restored and written down in a notebook at home (at the discretion of the teacher).
It is necessary to mention other possible ways of proving this theorem:
1. Draw one of the diagonals of the trapezoid and use the sign and property of the middle line of the triangle.

2. Run CF || BA and consider the parallelogram ABCF and DCF.

3. Run EF || BA and consider the equality of FND and ENC.

g) At this stage, homework is given: p. 84, textbook, ed. Atanasyan L.S. (proof of the property of the midline of a trapezoid in a vector way), write in a notebook.
h) We solve problems for using the definition and properties of the middle line of the trapezoid according to the finished drawings (see Appendix 2). Appendix 2 is given to each student, and the solution of problems is drawn up on the same sheet in a short form.

The area of the trapezoid. Greetings! In this publication, we will consider this formula. Why is it the way it is and how can you understand it? If there is an understanding, then you do not need to learn it. If you just want to see this formula and what is urgent, then you can immediately scroll down the page))
Now in detail and in order.
A trapezoid is a quadrilateral, two sides of this quadrilateral are parallel, the other two are not. Those that are not parallel are the bases of the trapezoid. The other two are called sides.
If the sides are equal, then the trapezoid is called isosceles. If one of the sides is perpendicular to the bases, then such a trapezoid is called rectangular.
In the classical form, the trapezoid is depicted as follows - the larger base is at the bottom, respectively, the smaller one is at the top. But no one forbids depicting it and vice versa. Here are the sketches:

The next important concept.
The median line of a trapezoid is a segment that connects the midpoints of the sides. The median line is parallel to the bases of the trapezoid and is equal to their half-sum.

Now let's delve deeper. Why exactly?
Consider a trapezoid with bases a and b and with the middle line l, and perform some additional constructions: draw straight lines through the bases, and perpendiculars through the ends of the midline until they intersect with the bases:

*Letter designations of vertices and other points are not entered intentionally to avoid unnecessary designations.
Look, triangles 1 and 2 are equal according to the second sign of equality of triangles, triangles 3 and 4 are the same. From the equality of triangles follows the equality of the elements, namely the legs (they are indicated respectively in blue and red).
Now attention! If we mentally “cut off” the blue and red segments from the lower base, then we will have a segment (this is the side of the rectangle) equal to the midline. Further, if we “glue” the cut off blue and red segments to the upper base of the trapezoid, then we will also get a segment (this is also the side of the rectangle) equal to the midline of the trapezoid.
Got it? It turns out that the sum of the bases will be equal to the two medians of the trapezoid:

See another explanation
Let's do the following - build a straight line passing through the lower base of the trapezoid and a straight line that will pass through points A and B:

We get triangles 1 and 2, they are equal in side and adjacent angles (the second sign of equality of triangles). This means that the resulting segment (in the sketch it is marked in blue) is equal to the upper base of the trapezoid.
Now consider a triangle:

*The median line of this trapezoid and the median line of the triangle coincide.
It is known that the triangle is equal to half of the base parallel to it, that is:

Okay, got it. Now about the area of the trapezoid.
Trapezium area formula:

They say: the area of a trapezoid is equal to the product of half the sum of its bases and height.
That is, it turns out that it is equal to the product of the midline and height:
You probably already noticed that this is obvious. Geometrically, this can be expressed as follows: if we mentally cut off triangles 2 and 4 from the trapezoid and put them on triangles 1 and 3, respectively:

Then we get a rectangle in area equal to the area of our trapezoid. The area of this rectangle will be equal to the product of the midline and height, that is, we can write:

But the point here is not in writing, of course, but in understanding.
Download (view) the material of the article in *pdf format
That's all. Good luck to you!
Sincerely, Alexander.

